Cho \[B = \left( { - 8} \right).25.{\left( { - 3} \right)^2}\] và \[C = \left( { - 30} \right).{\left( { - 2} \right)^3}.\left( {{5^3}} \right)\] . Chọn câu đúng
 Giải bởi Vietjack
Giải bởi Vietjack
Trả lời:
\[B = \left( { - 8} \right).25.{\left( { - 3} \right)^2} = - 200.9 = - 1800\]
\[\begin{array}{*{20}{l}}{C = \left( { - 30} \right).{{\left( { - 2} \right)}^3}.\left( {{5^3}} \right)}\\{ = \left( { - 30} \right).\left( { - 8} \right).125}\\{ = \left( { - 30} \right).\left( { - 1000} \right)}\\{ = 30000}\end{array}\]
Khi đó \[B.50 = - 1800.50 = - 90000;C.( - 3) = 30000.( - 3) = - 90000\]
Vậy \[B.50 = C.( - 3)\]
Đáp án cần chọn là: B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Ba bạn An, Bình, Cường chơi ném tiêu với bia gồm năm vòng như hình 3.19. Kết quả được ghi lại trong bảng sau:
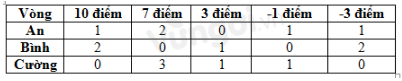
Sắp xếp tên các bạn theo thứ tự từ thấp đến cao là?
+) Tích của một số chẵn các số nguyên âm là một số nguyên ..(1)..
+) Tích của một số lẻ các số nguyên âm là một số nguyên ..(2)..
Từ thích hợp để điền vào hai chỗ chấm trên lần lượt là:
Khi \(x = - 12\) , giá trị của biểu thức \[(x - 8).(x + 7)\] là số nào trong bốn số sau:
Công ty Ánh Dương có lợi nhuận ở mỗi tháng trong Quý I là – 30 triệu đồng. Trong Quý II, lợi nhuận mỗi tháng của công ty là 70 triệu đồng. Sau 6 tháng đầu năm, lợi nhuận của công ty Ánh Dương là?
1. Nhân hai số nguyên khác dấu
Quy tắc nhân hai số nguyên khác dấu
Muốn nhân hai số nguyên khác dấu, ta nhân phần số tự nhiên của hai số đó với nhau rồi đặt dấu “-” trước kết quả nhận được.
Nếu m, n ∈ N* thì m.(-n) = (-n).m = - (m.n).
Ví dụ 1. Thực hiện phép nhân sau:
a) (-23).12; b) 134.(-25); c) 6.(-32).
Lời giải
a) (-23).12 = - (23.12) = -276;
b) 134.(-25) = - (134.25) = - 3350;
c) 6.(-32) = - (6.32) = -192.
2. Nhân hai số nguyên cùng dấu
Quy tắc nhân hai số nguyên âm
Muốn nhân hai số nguyên âm, ta nhân phần số tự nhiên của hai số đó với nhau.
Nếu m, n ∈ N* thì (-m).(-n) = (-n).(-m) = m.n.
Ví dụ 2. Thực hiện các phép nhân sau:
a) (-12).(-32); b) (-138).(-25); c) (-10).(-5 134).
Lời giải
a) (-12).(-32) = 12.32 = 384;
b) (-138).(-25) = 138.25 = 3450;
c) (-10).(-5 134) = 10. 5 134 = 51 340.
3. Tính chất của phép nhân
Phép nhân các số nguyên có các tính chất:
Giao hoán: a.b = b.a;
Kết hợp: (a.b).c = a.(b.c);
Phân phối của phép nhân đối với phép cộng: a.(b + c) = a.b + a.c.
Ví dụ 3. Tính một cách hợp lí:
a) (125).(-134).(-8);
b) 12.(-27) + 12.(-73);
c) 4.(1 930 + 2 019) + 4.(-2 019).
Lời giải
a) (125).(-134).(-8)
= [125.(-8)].(-134)
= (-1000).(-134)
= 134 000.
b) 12.(-27) + 12.(-73)
= 12.[(-27) + (-73)]
= 12. (-100)
= - 1 200.
c) 4.(1 930 + 2 019) + 4.(-2 019)
= 4.1 930 + 4.2 019 + 4.(-2 019)
= 4.1 930 + [4.2 019 + 4.(-2 019)]
= 4.1 930 + 4.[2019 + (-2 019)]
= 4.1 930 + 4.0
= 7 720.