Chọn câu đúng:

1. Chu vi, diện tích của hình vuông, hình chữ nhật, hình thang 

Công thức:

Hình vuông cạnh a:

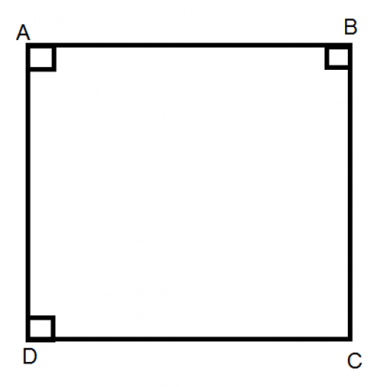
Chu vi: C = 4a.

Diện tích: S = a².

Hình chữ nhật có chiều dài là a, chiều rộng là b:

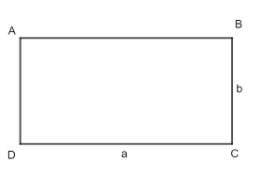
Chu vi: C = 2(a + b).

Diện tích: S = a.b.

Hình thang có độ dài hai cạnh đáy là a, b chiều cao h:

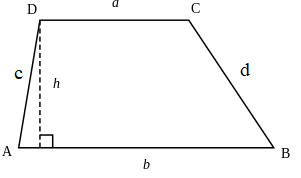
Chu vi: C = a + b + c + d.

Diện tích: S = (a + b).h:2.

Ví dụ 1. Bác Khôi muốn lát nền cho một căn phòng hình chữ nhật có chiều dài 6m, chiều rộng 3m. Loại gạch lát nền được sử dụng là hình vuông có cạnh 30cm. Hỏi bác Khôi phải sử dụng bao nhiêu viên gạch (coi mạch vữa không đáng kể).

Lời giải

Diện tích căn phòng hình chữ nhật là: 6.3 = 18 (m²).

Diện tích một viên gạch lát nền là: 30.30 = 900(cm²).

Đổi 18 m² = 180 000 (cm²).

Số viên gạch cần để lát đủ căn phòng là: 180 000:900 = 200 (viên).

Ví dụ 2. Một thửa ruộng có dạng như hình bên. Nếu trên mỗi mét vuông thu hoạch được 0,8kg thóc thì thửa ruộng đó thu hoạch được bao nhiêu ki – lô – gam thóc?

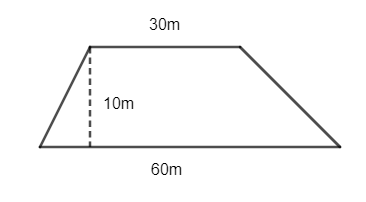
Lời giải

Diện tích thửa ruộng hình thang là: (60 + 30).10:2 = 450 (m²).

Trên thửa ruộng đó thu hoạch được số ki – lô – gam thóc là: 450.0,8 = 360 (kg).

Vậy trên thửa ruộng đó thu hoạch được 360 ki – lô – gam thóc.

2. Chu vi, diện tích hình bình hành, hình thoi.

Hình bình hành: 

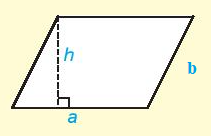
Chu vi: C = 2(a + b).

Diện tích: S = a.h.

Hình thoi:

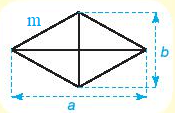
Chu vi: C = 4.m.

Diện tích: S = 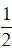ab .

Ví dụ 3. Trên một mảnh đất hình chữ nhật có chiều dài 12m, chiều rộng 10m.

a) Người nông dân định làm một tường rào bao quanh khu vườn. Hỏi tường rào đó dài bao nhiêu m?

b) Trên khu vườn nó người nông dân phân chia khu vực để trồng hoa, trồng cỏ như hình bên. Hoa sẽ được trồng ở khu vực hình bình hành AMCN, cỏ sẽ được trồng ở phần đất còn lại. Tính diện tích trồng hoa và trồng cỏ.

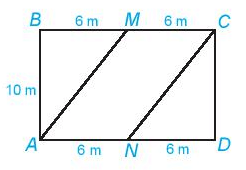
Lời giải

a) Chu vi của khu vườn hình chữ nhật là: 2.(12 + 10) = 2.22 = 44 (m).

Vậy độ dài của tường rào là: 44m.

b) Diện tích trồng hoa là: 6.10 = 60 (m²).

Diện tích khu vườn hình chữ nhật: 12.10 = 120 (m²).

Diện tích trồng cỏ là: 120 – 60 = 60 (m²).

Ví dụ 4. Hình thoi MNPQ có độ dài hai đường chéo 5m và 4m. Diện tích hình thoi MNPQ bằng bao nhiêu?

Lời giải

Diện tích hình thoi MNPQ là: 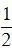.5.4 = 10(m²) .

Vậy diện tích hình thoi MNPQ là 10 m².