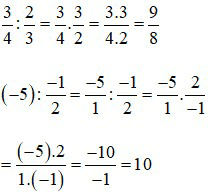Tìm x biết \[x:\left( { - \frac{2}{5}} \right) = \frac{3}{{54}}\]
Giải bởi Vietjack
Trả lời:
\[x:\left( { - \frac{2}{5}} \right) = \frac{3}{{54}}\]
\[x = \frac{3}{{54}}.\left( { - \frac{2}{5}} \right)\]
\[x = \frac{1}{{18}}.\frac{{ - 2}}{5}\]
\[x = \frac{{ - 1}}{{45}}\]
Đáp án cần chọn là: D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Điền số thích hợp vào ô trống
Chim ruồi ong hiện là loài chim bé nhỏ nhất trên Trái Đất với chiều dài chỉ khoảng 5 cm. Chim ruồi “khổng lồ” ở Nam Mỹ là thành viên lớn nhất của gia đình chim ruồi trên thế giới, nó dài gấp \[\frac{{33}}{8}\] lần chim ruồi ong. Chiều dài của chim ruồi “khổng lồ” ở Nam Mỹ là cm
Điền số thích hợp vào ô trống:
Một ô tô chạy hết \[\frac{3}{4}\] giờ trên một đoạn đường với vận tốc trung bình 40km/h.
Người lái xe muốn thời gian chạy hết đoạn đường đó chỉ \[\frac{1}{2}\] giờ thì ô tô phải chạy với vận tốc trung bình là: km/h
Tính diện tích một hình tam giác biết hai cạnh góc vuông của tam giác đó lần lượt là \[\frac{5}{3}cm\] và \[\frac{7}{4}cm\]?
Tính giá trị của biểu thức
\[\left( {\frac{{ - 2}}{{ - 5}}:\frac{3}{{ - 4}}} \right).\frac{4}{5}\]
Điền số thích hợp vào ô trống
Độ cao của đáy vịnh Cam Ranh là -32 m. Độ cao của đáy sông Sài Gòn bằng \[\frac{5}{8}\] ở độ cao của đáy vịnh Cam Ranh. Vậy độ cao của đáy sông Sài Gòn là
mét
Một hình chữ nhật có diện tích là \[\frac{8}{{15}}\left( {c{m^2}} \right)\], chiều dài là \[\frac{4}{3}\left( {cm} \right)\]. Tính chi vu hình chữ nhật đó.
Tính giá trị biểu thức \[A = \left( {\frac{{11}}{4}.\frac{{ - 5}}{9} - \frac{4}{9}.\frac{{11}}{4}} \right).\frac{8}{{33}}\]
Rút gọn \[N = \frac{{\frac{4}{{17}} - \frac{4}{{49}} - \frac{4}{{131}}}}{{\frac{3}{{17}} - \frac{3}{{49}} - \frac{3}{{131}}}}\] ta được
1. Phép nhân hai phân số
– Muốn nhân hai phân số, ta nhân các tử số với nhau và các mẫu số với nhau.
Cho a, b, c, d ∈ ℤ; b≠0; d≠0.
Khi đó phép nhân hai phân số ta có:
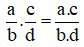
Ví dụ 1:
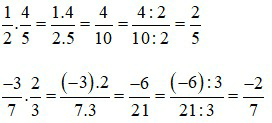
2. Tính chất của phép nhân
Cho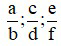
là các phân số với a, b, c, d, e, f ∈ ℤ; b≠0; d≠0; f≠0.
Khi đó ta có các tính chất của phép nhân như sau:
+ Tính giao hoán: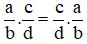
+ Tính kết hợp: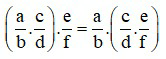
+ Tính nhân với 1: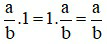
+ Tính phân phối giữa phép nhân với phép cộng: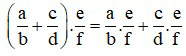
Ví dụ 2:
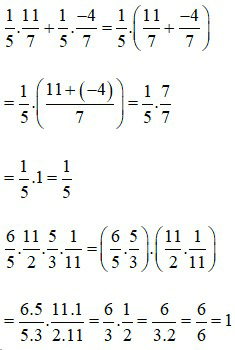
3. Phép chia phân số
a) Phân số nghịch đảo:
Phân số này được gọi là nghịch đảo của phân số kia nếu tích của chúng bằng 1
Cho a, b ∈ ℤ; a, b ≠ 0
Phân số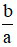 
là phân số nghịch đảo của phân số
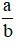vì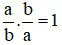
Ví dụ 3:
Phân số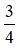 
là phân số nghịch đảo của phân số 
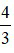vì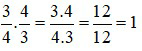 
b) Phép chia phân số
– Muốn chia một phân số cho một phân số khác 0, ta nhân số bị chia với phân số nghịch đảo của số chia.
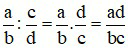với a, b, c, d ∈ ℤ; b≠0; c≠0; d≠0
Ví dụ 4:
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số chẵn
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 2
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
