Cho \[P = \left( {\frac{7}{{20}} + \frac{{11}}{{15}} - \frac{{15}}{{12}}} \right):\left( {\frac{{11}}{{20}} - \frac{{26}}{{45}}} \right)\] và \[Q = \frac{{5 - \frac{5}{3} + \frac{5}{9} - \frac{5}{{27}}}}{{8 - \frac{8}{3} + \frac{8}{9} - \frac{8}{{27}}}}:\frac{{15 - \frac{{15}}{{11}} + \frac{{15}}{{121}}}}{{16 - \frac{{16}}{{11}} + \frac{{16}}{{121}}}}\]. Chọn kết luận đúng:
 Giải bởi Vietjack
Giải bởi Vietjack
Trả lời:
\[P = \left( {\frac{7}{{20}} + \frac{{11}}{{15}} - \frac{{15}}{{12}}} \right):\left( {\frac{{11}}{{20}} - \frac{{26}}{{45}}} \right)\]
\[P = \left( {\frac{{21}}{{60}} + \frac{{44}}{{60}} - \frac{{75}}{{60}}} \right):\left( {\frac{{99}}{{180}} - \frac{{104}}{{180}}} \right)\]
\[P = \frac{{ - 10}}{{60}}:\frac{{ - 5}}{{180}} = \frac{{ - 10}}{{60}}.\frac{{180}}{{ - 5}} = 6\]
\[Q = \frac{{5 - \frac{5}{3} + \frac{5}{9} - \frac{5}{{27}}}}{{8 - \frac{8}{3} + \frac{8}{9} - \frac{8}{{27}}}}:\frac{{15 - \frac{{15}}{{11}} + \frac{{15}}{{121}}}}{{16 - \frac{{16}}{{11}} + \frac{{16}}{{121}}}}\]
\[Q = \frac{{5\left( {1 - \frac{5}{3} + \frac{1}{9} - \frac{1}{{27}}} \right)}}{{8\left( {1 - \frac{1}{3} + \frac{1}{9} - \frac{1}{{27}}} \right)}}:\frac{{15\left( {1 - \frac{1}{{11}} + \frac{1}{{121}}} \right)}}{{16\left( {1 - \frac{1}{{11}} + \frac{1}{{121}}} \right)}}\]
\[Q = \frac{5}{8}:\frac{{15}}{{16}} = \frac{5}{8}.\frac{{16}}{{15}} = \frac{2}{3}\]
Vì \[6 > \frac{2}{3}\] nên P > Q
Đáp án cần chọn là: A
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Điền số thích hợp vào ô trống:
Một ô tô chạy hết \[\frac{3}{4}\] giờ trên một đoạn đường với vận tốc trung bình 40km/h.
Người lái xe muốn thời gian chạy hết đoạn đường đó chỉ \[\frac{1}{2}\] giờ thì ô tô phải chạy với vận tốc trung bình là: km/h
Có bao nhiêu giá trị của x thỏa mãn \[\left( {\frac{7}{6} + x} \right):\frac{{16}}{{25}} = \frac{{ - 5}}{4}\]:
Phân số \[\frac{a}{b}\] là phân số lớn nhất mà khi chia mỗi phân số \[\frac{{12}}{{35}};\frac{{18}}{{49}}\]cho \[\frac{a}{b}\] ta được kết quả là một số nguyên. Tính a + b.
Tính: \[\frac{{28}}{{15}}.\frac{1}{{{4^2}}}.3 + \left( {\frac{8}{{15}} - \frac{{69}}{{60}}.\frac{5}{{23}}} \right):\frac{{51}}{{54}}\]
Một người đi xe máy, đi đoạn đường AB với vận tốc 40km/h hết \[\frac{5}{4}\] giờ. Lúc về, người đó đi với vận tốc 45km/h. Tính thời gian người đó đi từ B về A?
Có bao nhiêu giá trị nguyên dương của x thỏa mãn \[{\left( {\frac{{ - 5}}{3}} \right)^3} < x < \frac{{ - 24}}{{35}}.\frac{{ - 5}}{6}\]?
Giá trị nào dưới đây của x thỏa mãn \[x:\frac{5}{8} = \frac{{ - 14}}{{35}}.\frac{{15}}{{ - 42}}\]
Giá trị nào dưới đây của x thỏa mãn \[\left( { - \frac{3}{5}} \right).x = \frac{4}{{15}}\]?
Để làm bánh caramen, Linh cần \[\frac{4}{5}\] cốc đường để làm được 10 cái bánh. Vậy muốn làm 1515 cái bánh thì Linh cần bao nhiêu cốc đường?
1. Phép nhân hai phân số
– Muốn nhân hai phân số, ta nhân các tử số với nhau và các mẫu số với nhau.
Cho a, b, c, d ∈ ℤ; b≠0; d≠0.
Khi đó phép nhân hai phân số ta có:
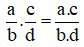
Ví dụ 1:
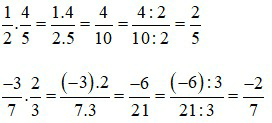
2. Tính chất của phép nhân
Cho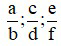 là các phân số với a, b, c, d, e, f ∈ ℤ; b≠0; d≠0; f≠0.
là các phân số với a, b, c, d, e, f ∈ ℤ; b≠0; d≠0; f≠0.
Khi đó ta có các tính chất của phép nhân như sau:
+ Tính giao hoán: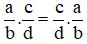
+ Tính kết hợp: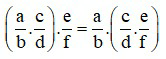
+ Tính nhân với 1: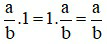
+ Tính phân phối giữa phép nhân với phép cộng: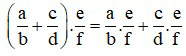
Ví dụ 2:
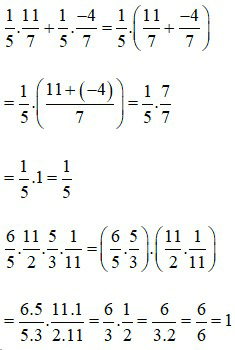
3. Phép chia phân số
a) Phân số nghịch đảo:
Phân số này được gọi là nghịch đảo của phân số kia nếu tích của chúng bằng 1
Cho a, b ∈ ℤ; a, b ≠ 0
Phân số 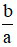 là phân số nghịch đảo của phân số
là phân số nghịch đảo của phân số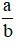 vì
vì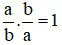
Ví dụ 3:
Phân số 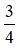 là phân số nghịch đảo của phân số
là phân số nghịch đảo của phân số 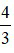 vì
vì 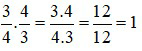
b) Phép chia phân số
– Muốn chia một phân số cho một phân số khác 0, ta nhân số bị chia với phân số nghịch đảo của số chia.
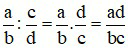 với a, b, c, d ∈ ℤ; b≠0; c≠0; d≠0
với a, b, c, d ∈ ℤ; b≠0; c≠0; d≠0
Ví dụ 4: