Bạn Thu đọc một cuốn sách trong 4 ngày. Ngày thứ nhất Thu đọc được \[\frac{1}{5}\] cuốn sách và 10 trang. Ngày thứ hai, Thu đọc được \[\frac{4}{9}\] số trang còn lại và 10 trang. Ngày thứ ba, Thu đọc được \[\frac{2}{7}\] số trang còn lại và 10 trang. Ngày thứ tư, Thu đọc được \[\frac{8}{9}\] số trang còn lại và 10 trang cuối cùng. Hỏi cuốn sách Thu đã đọc có bao nhiêu trang?
 Giải bởi Vietjack
Giải bởi Vietjack
Trả lời
10 trang là: \[\left( {1 - \frac{8}{9}} \right) = \frac{1}{9}\]số trang đọc trong ngày thứ tư.
Vậy số trang sách còn lại sau ngày thứ ba là: \[10:\frac{1}{9} = 90\] (trang).
(90+10)=100 trang là: \[\left( {1 - \frac{2}{7}} \right) = \frac{5}{7}\]số trang sách còn lại sau ngày thứ hai.
Vậy số trang sách còn lại sau ngày thứ hai là: \[100:\frac{5}{7} = 140\] (trang).
(140+10)=150 trang là: \[\left( {1 - \frac{4}{9}} \right) = \frac{5}{9}\]số trang sách còn lại sau ngày thứ nhất.
Vậy số trang sách còn lại sau ngày thứ nhất là: \[150:\frac{5}{9} = 270\] (trang).
(270+10)=280 trang là \[\left( {1 - \frac{1}{5}} \right) = \frac{4}{5}\]số trang của cả cuốn sách.
Số trang của cả cuốn sách Thu đọc là: \[280:\frac{4}{5} = 350\] (trang).
Vậy cuốn sách Thu đọc có 350 trang.
Đáp án cần chọn là: C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Bạn An tham gia đội hoạt động tình nguyện thu gom và phân loại rác thải trong xóm. Hết ngày, An thu được 9 kg rác khó phân huỷ và 12 kg rác dễ phân huỷ. Số rác khó phân huỷ bạn An thu được bằng \[\frac{3}{{20}}\] số rác khó phân huỷ cả đội thu được. Đội của An thu được tất cả bao nhiêu ki-lô-gam rác khó phân huỷ?
Tổng số đo chiều dài của ba tấm vải là 224m. Nếu cắt \[\frac{3}{7}\] tấm vải thứ nhất, \[\frac{1}{5}\] tấm vải thứ hai và \[\frac{2}{5}\] tấm vải thứ ba thì phần còn lại của ba tấm vải bằng nhau. Tính chiều dài tấm vải thứ nhất.
Số sách ở ngăn A bằng \[\frac{2}{3}\] số sách ở ngăn B. Nếu chuyển 3 quyển từ ngăn A sang ngăn B thì số sách ở ngăn A bằng \[\frac{3}{7}\] số sách ở ngăn B. Tìm số sách lúc đầu ở ngăn B.
Số thỏ ở chuồng A bằng \[\frac{2}{5}\] tổng số thỏ ở cả hai chuồng A và B. Sau khi bán 3 con ở chuồng A thì số thỏ ở chuồng A bằng \[\frac{1}{3}\] tổng số thỏ ở hai chuồng lúc đầu. Tính số thỏ lúc đầu ở chuồng B.
Một đội công nhân sửa một đoạn đường trong ba ngày: ngày thứ nhất sửa \[\frac{5}{9}\] đoạn đường, ngày thứ hai sửa \[\frac{1}{4}\] đoạn đường. Ngày thứ ba đội sửa nốt 7m còn lại. Hỏi đoạn đường dài bao nhiêu mét?
Một người mang một số trứng ra chợ bán. Buổi sáng bán được \[\frac{3}{5}\] số trứng mang đi. Buổi chiều bán thêm được 3939 quả. Lúc về còn lại số trứng bằng \[\frac{1}{8}\] số trứng đã bán. Hỏi người đó mang tất cả bao nhiêu quả trứng đi bán?
Một cửa hàng có hai thùng dầu. Biết \[\frac{2}{3}\] số dầu ở thùng thứ nhất là 28 lít dầu, \[\frac{4}{5}\]số dầu ở thùng thứ hai là 48 lít dầu. Hỏi cả hai thùng dầu có tất cả bao nhiêu lít dầu?
Tìm chiều dài của một đoạn đường, biết rằng \[\frac{4}{7}\] đoạn đường đó dài 40km.
Tìm diện tích của một hình chữ nhật, biết rằng \[\frac{3}{8}\] chiều dài là 12cm, \[\frac{2}{3}\]chiều rộng là 12cm.
Hai đám ruộng thu hoạch tất cả 990kg990kg thóc. Biết rằng \[\frac{2}{3}\] số thóc thu hoạch ở ruộng thứ nhất bằng \[\frac{4}{5}\] số thóc thu hoạch ở ruộng thứ hai. Hỏi đám ruộng thứ hai thu hoạch bao nhiêu thóc?
Một bác nông dân vừa thu hoạch 30 kg cà chua và 12 kg đậu đũa. Bác đem \[\frac{4}{5}\] ở số cà chua đó đi bán, giá mỗi ki-lô-gam cà chua là 12 500 đồng. Hỏi bác nông dân nhận được bao nhiêu tiền?
Biết \[\frac{3}{5}\] số học sinh giỏi của lớp 6A là 12 học sinh. Hỏi lớp 6A có bao nhiêu học sinh giỏi?
Minh đọc quyển sách trong 4 ngày. Ngày thứ nhất Minh đọc được \[\frac{2}{5}\] số trang sách. Ngày thứ hai Minh đọc được \[\frac{3}{5}\] số trang sách còn lại. Ngày thứ ba đọc được 80% số trang sách còn lại sau ngày thứ hai và ngày thứ tư đọc 30 trang cuối cùng. Hỏi cuốn sách đó có bao nhiêu trang?
1. Tìm giá trị phân số của một số cho trước
Muốn tìm 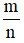 của một số a cho trước ta tính
của một số a cho trước ta tính 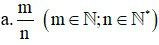
Ví dụ 1: 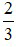 của 30 là
của 30 là 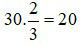
2. Tìm một số khi biết giá trị phân số của nó
– Muốn tìm một số biết 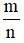 của số đó bằng b, ta tính
của số đó bằng b, ta tính 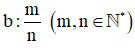
Ví dụ 2: Một người đi ra chợ để mua vải, người đó mua 25m vải ứng với 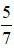 cuộn vải. Hỏi cuộn vải ban đầu dài bao nhiêu m.
cuộn vải. Hỏi cuộn vải ban đầu dài bao nhiêu m.
Lời giải:
Độ dài cuộn vải ban đầu là:
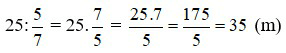
Vậy cuộn vải ban đầu dài 35m.