Cho tam giác IHK đều có G là trọng tâm. Khẳng định nào sau đây là đúng?
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
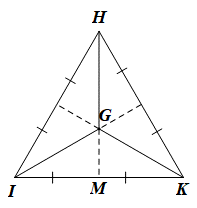
Gọi M là trung điểm của IK.
• Xét DHIM và DHKM có:
HI = HK (do DIHK đều),
HM và cạnh chung,
IM = KM (do M là trung điểm của IK).
Do đó DHIM = DHKM (c.c.c).
Suy ra \(\widehat {HMI} = \widehat {HMK}\) (hai góc tương ứng).
Mà \(\widehat {HMI} + \widehat {HMK} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {HMI} = \widehat {HMK} = \frac{{180^\circ }}{2} = 90^\circ \) hay HG ⊥ IK.
Chứng minh tương tự ta cũng có IG ⊥ HK và KG ⊥ IH.
• Xét DHIG có HK ⊥ IG, IK ⊥ HG, KG ⊥ HI.
Nên HK, IK, KG là ba đường cao của tam giác HIG.
Mà HK, IK, KG cắt nhau tại K.
Suy ra K là trực tâm tam giác GIH.
Vậy ta chọn phương án C.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác MNP có \(\widehat M = 63^\circ ,\widehat N = 48^\circ \). Vẽ trực tâm O của tam giác MNP. Số đo góc MON là:
Cho tam giác ABC vuông tại A, trên tia BA lấy M sao cho BM = BC. Tia phân giác góc B cắt AC tại H. Khẳng định nào sau đây là sai?
Cho tam giác ABC nhọn có đường cao AI. Trên AI lấy E sao cho \(\widehat {BAI} = \widehat {BCE}.\) Gọi F là giao điểm của AB và CE, H là giao điểm của BE và AC. Khẳng định nào sau đây là sai?
Cho tam giác XYZ nhọn, đường cao XA. Lấy B thuộc đoạn AZ, vẽ BC vuông góc XZ. Giao điểm của XA và BC là I. Khẳng định nào sau đây là đúng?
Cho tam giác ABC có \(\widehat B = 50^\circ ,\widehat C = 30^\circ \). Vẽ đường cao AH, phân giác AE. Trên cạnh AC lấy D sao cho \(\widehat {CB{\rm{D}}} = 10^\circ \). Gọi I là giao điểm của AE và BD. Số đo góc AID là: