Cho tam giác ABC nhọn, đường cao AH. Lấy điểm D sao cho AB là trung trực của HD. Lấy điểm E sao cho AC là trung trực của HE. Gọi M là giao điểm của DE và AB, gọi N là giao điểm của DE và AC. Khẳng định nào sau đây là đúng?
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: C
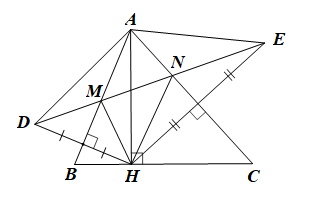
Xét DDHE có AB, AC là hai đường trung trực của tam giác cắt nhau tại A nên A cách đều ba đỉnh của tam giác
Do đó AD = AH = AE.
Tam giác ADE có AD = AE nên là tam giác cân tại A.
Suy ra \(\widehat {ADE} = \widehat {AED}\) (tính chất tam giác cân) (1)
Xét DADM và DAHM có
AM là cạnh chung,
DM = HM (do M thuộc trung trực của DH),
AD = AH (chứng minh trên).
Do đó DADM = DAHM (c.c.c).
Suy ra \(\widehat {ADM} = \widehat {AHM}\)(hai góc tương ứng) (2)
Xét DANH và DANE có
AN là cạnh chung,
NH = NE (do N thuộc trung trực của EH),
AH = AE (chứng minh trên)
Do đó DANH = DANE (c.c.c)
Suy ra \(\widehat {AHN} = \widehat {AEN}\)(hai góc tương ứng) (3)
Từ (1), (2) và (3) suy ra \(\widehat {AHN} = \widehat {AHM}\)
Do đó HA là tia phân giác của góc MHN.
Vậy ta chọn phương án C.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho góc nhọn \(\widehat {xOy}\), trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Đường trung trực của OA và đường trung trực của OB cắt nhau tại I.
Cho các khẳng định sau:
(I) OI là tia phân giác của \(\widehat {xOy}\);
(II) OI là đường trung trực của đoạn AB.
Chọn khẳng định đúng:
Cho tam giác DEF có DM, EN là hai đường trung tuyến cắt nhau tại G. Kéo dài DM lấy điểm H sao cho MH = MD. Kéo dài EN lấy điểm K sao cho NK = NE. Chọn khẳng định sai?
Cho tam giác ABD có AB < AD < BD và \(\widehat {ADB} = 32^\circ \). Trên cạnh BD lấy điểm C sao cho AB = CA = CB. Số đo của \(\widehat {{\rm{CAD}}}\) là
Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba có thể là độ dài ba cạnh của một tam giác là
Cho tam giác DEF có \(\widehat D = 38^\circ \) và \(\widehat E = 110^\circ .\) Độ dài các cạnh của ∆DEF sắp xếp theo thứ tự tăng dần là
Cho tam giác ABC có AH, BK, CL lần lượt là ba đường cao của tam giác ABC. Chọn khẳng định đúng:
Cho tam giác AOM có \(\widehat A = 52^\circ \). Ba đường phân giác cắt nhau tại I. Số đo góc MIO là:
Cho ∆ABC vuông tại A. Trên cạnh AC lấy điểm M bất kì (M ≠ A, C). Qua M kẻ đường thẳng vuông góc với BC tại N. Từ C kẻ đường thẳng vuông góc với BM tại P. Gọi D là giao điểm của AB và CP. Khẳng định nào sau đây sai?
Cho ∆ABC cân tại A có BC = 9 cm; chu vi ∆ABC bằng 25 cm. Chọn khẳng định sai:
Sau khi đo bằng thước đo góc bạn An đã điền số đo các góc vào hai hình vẽ như sau:
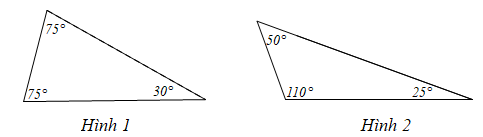
Chọn khẳng định đúng:
Cho tam giác MNP có trung tuyến MA, NC cắt nhau tại O. Biết MO = 2,5 cm, OC = 1 cm. Độ dài các đường trung tuyến MA, NC lần lượt là:
