Trắc nghiệm Toán 7 CTST Bài tập cuối chương 8 có đáp án (Phần 2) (Thông hiểu)
-
1082 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Sau khi đo bằng thước đo góc bạn An đã điền số đo các góc vào hai hình vẽ như sau:
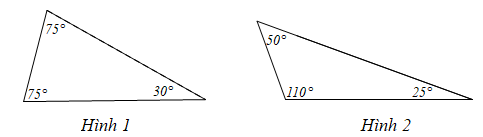
Chọn khẳng định đúng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Xét Hình 1: Ta có \(\widehat {\rm{A}} + \widehat {\rm{B}} + \widehat {\rm{C}} = 75^\circ + 75^\circ + 30^\circ = 180^\circ \).
Xét Hình 2: Ta có \(\widehat {\rm{D}} + \widehat {\rm{E}} + \widehat {\rm{F}} = 50^\circ + 110^\circ + 25^\circ = 185^\circ \).
Mà tổng số đo ba góc của một tam giác bằng 180°.
Vậy bạn An đã đo đúng Hình 1 và đo nhầm Hình 2.
Vậy ta chọn phương án A.
Câu 2:
Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba có thể là độ dài ba cạnh của một tam giác là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có “Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng độ dài của hai cạnh còn lại”
Vì 6 cm < 2 cm + 3 cm = 5 cm, nên A sai;
8 cm = 4 cm + 4 cm, nên B sai;
8 cm = 5 cm + 3 cm, nên D sai;
7 cm – 5 cm < 9 cm < 7 cm + 5 cm, nên C đúng.
Vậy ta chọn phương án C.
Câu 3:
Cho hình vẽ
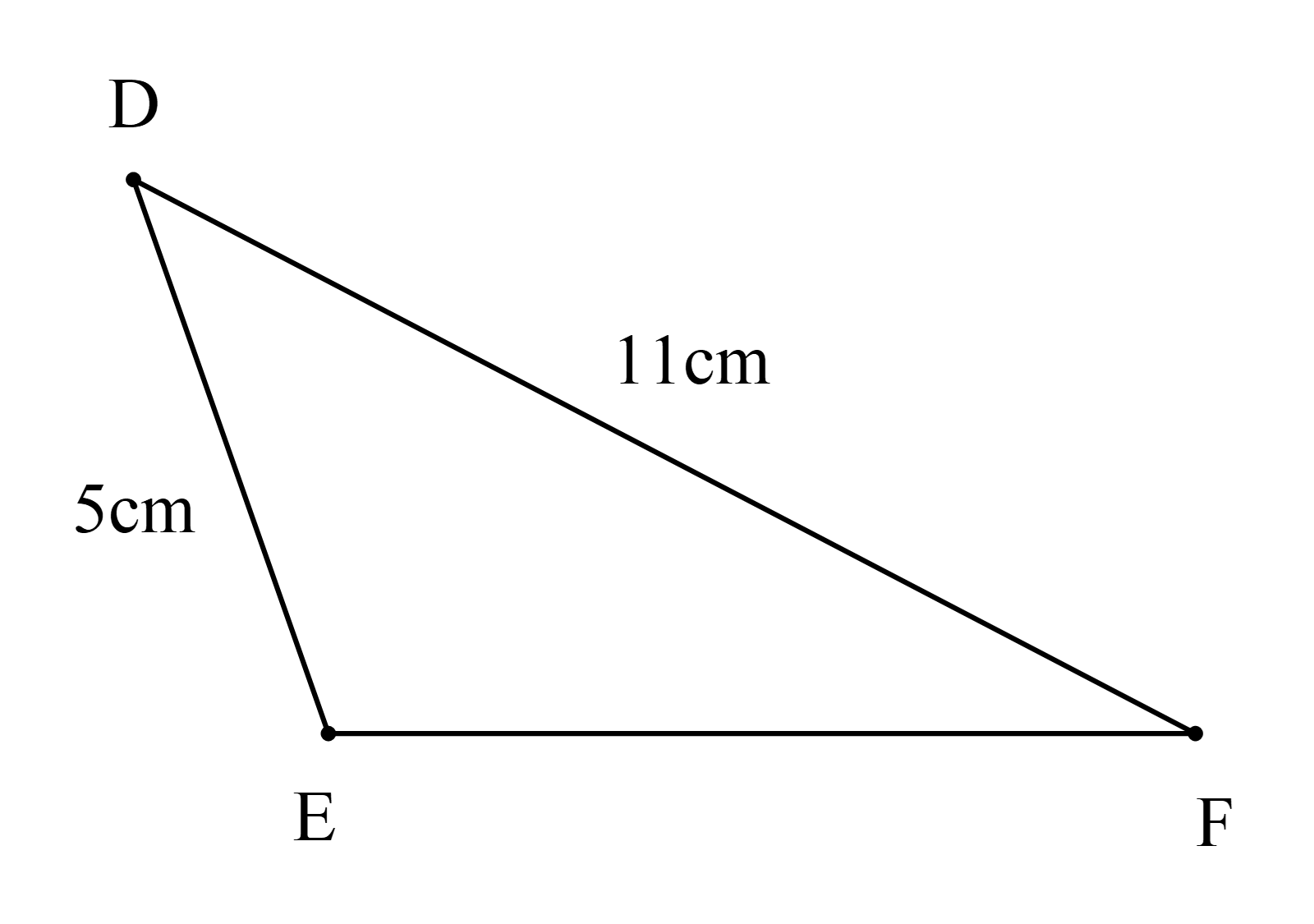
Độ dài cạnh EF là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Vì “Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng độ dài của hai cạnh còn lại”
Áp dụng bất đẳng thức cho ∆DEF ta có:
DF – DE < EF < DF + DE
Do đó 11 – 5 < EF < 11 + 5
Hay 6 < EF < 16.
Trong 4 phương án ta thấy EF = 8 cm thỏa mãn điều kiện trên.
Vậy ta chọn phương án D.
Câu 4:
Cho hình vẽ

Số đo của \(\widehat {AFO}\) là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Xét ∆FOB và ∆EOC có:
\(\widehat {FOB} = \widehat {{\rm{EOC}}}\) (hai góc đối đỉnh);
OB = OC (giả thiết);
\(\widehat {{\rm{FBO}}} = \widehat {{\rm{ECO}}}\) (giả thiết).
Suy ra ∆FOB = ∆EOC (g.c.g)
Suy ra \(\widehat {{\rm{BFO}}} = \widehat {{\rm{CEO}}} = 88^\circ \) (hai góc tương ứng)
Ta có \(\widehat {{\rm{BFO}}} + \widehat {AFO} = 180^\circ \) (hai góc kề bù)
Hay \(88^\circ + \widehat {AFO} = 180^\circ \)
Suy ra \(\widehat {AFO} = 180^\circ - 88^\circ = 92^\circ \).
Vậy ta chọn phương án C.
Câu 5:
Cho tam giác ABD có AB < AD < BD và \(\widehat {ADB} = 32^\circ \). Trên cạnh BD lấy điểm C sao cho AB = CA = CB. Số đo của \(\widehat {{\rm{CAD}}}\) là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
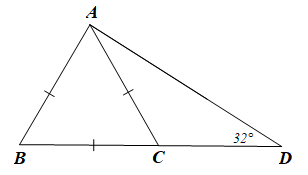
Theo hình vẽ ta có: AB = AC = BC
Suy ra ∆ABC là tam giác đều.
Suy ra \(\widehat {{\rm{ACB}}} = 60^\circ \) (tính chất tam giác đều)
Ta có \(\widehat {{\rm{ACB}}} + \widehat {{\rm{ACD}}} = 180^\circ \) (hai góc kề nhau)
Hay \(60^\circ + \widehat {{\rm{ACD}}} = 180^\circ \)
Suy ra \(\widehat {{\rm{ACD}}} = 180^\circ - 60^\circ = 120^\circ \)
Xét ∆ACD có: \(\widehat {{\rm{CAD}}} + \widehat {{\rm{ACD}}} + \widehat {\rm{D}} = 180^\circ \) (tổng ba góc trong tam giác bằng 180°)
Hay \(\widehat {{\rm{CAD}}} + 120^\circ + 32^\circ = 180^\circ \)
Suy ra \(\widehat {{\rm{CAD}}} = 180^\circ - 120^\circ - 32^\circ = 28^\circ \)
Vậy ta chọn phương án C.
Câu 6:
Cho hình vẽ sau:
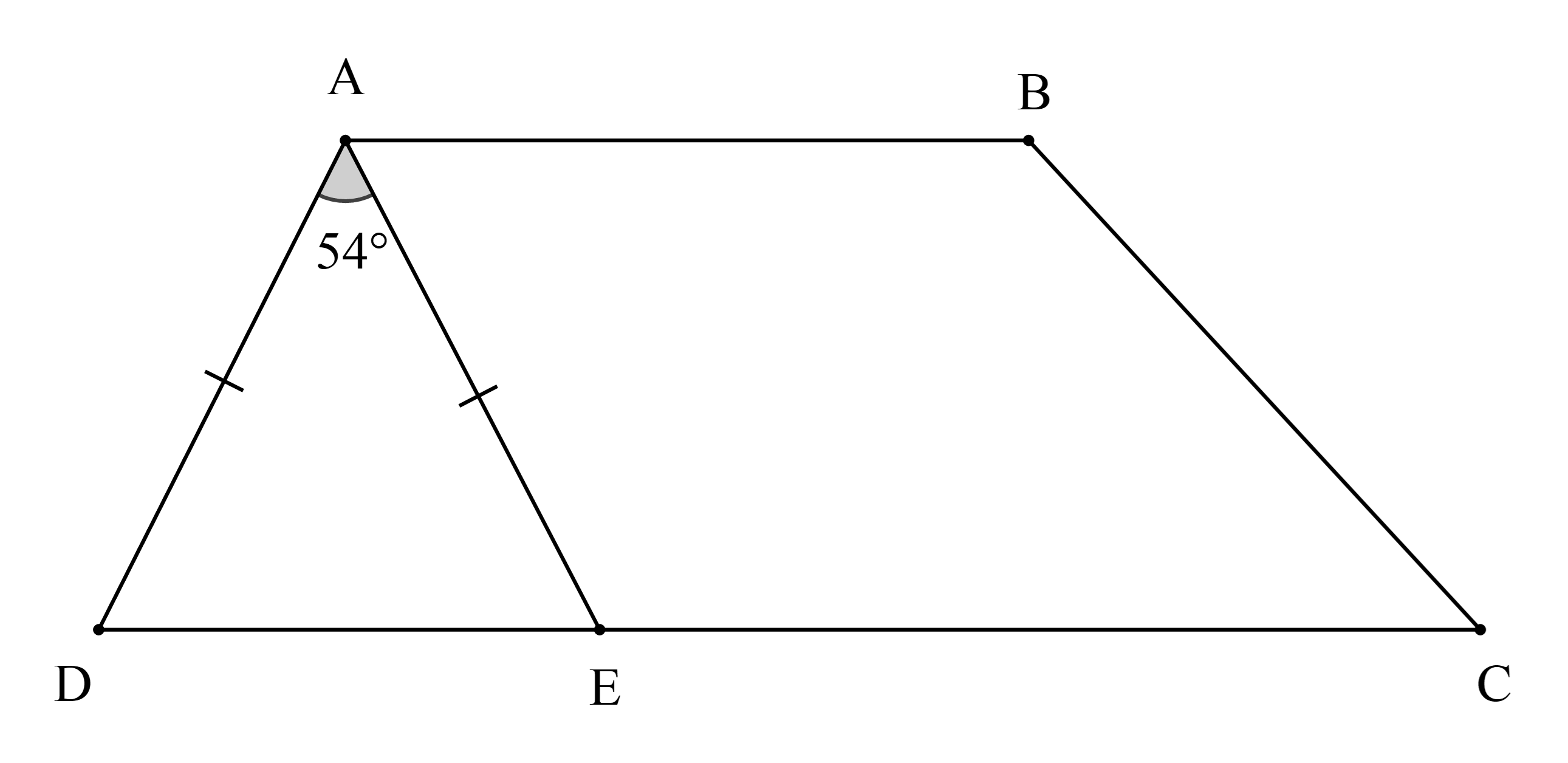
Số đo của \(\widehat {{\rm{BAE}}}\) là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Xét ∆ADE có AD = AE (giả thiết) nên ∆ADE cân tại A.
Suy ra \(\widehat {\rm{D}} = \widehat {{\rm{AED}}}\) (1)
Xét ∆AED có: \(\widehat {\rm{D}} + \widehat {{\rm{AED}}} + \widehat {{\rm{EAD}}} = 180^\circ \)(tổng ba góc trong tam giác bằng 180°)
Hay \(\widehat {\rm{D}} + \widehat {{\rm{AED}}} + 54^\circ = 180^\circ \)
Suy ra \(\widehat {\rm{D}} + \widehat {{\rm{AED}}} = 180^\circ - 54^\circ = 126^\circ \) (2)
Từ (1) và (2) suy ra \(\widehat {\rm{D}} = \widehat {{\rm{AED}}} = \frac{{126^\circ }}{2} = 63^\circ \)
Vì AB // CD do đó \(\widehat {{\rm{BAE}}} = \widehat {{\rm{AED}}} = 63^\circ \) (hai góc so le trong).
Vậy ta chọn phương án B.
Câu 7:
Cho tam giác DEF có \(\widehat D = 38^\circ \) và \(\widehat E = 110^\circ .\) Độ dài các cạnh của ∆DEF sắp xếp theo thứ tự tăng dần là
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A

Xét ∆DEF có: \(\widehat {\rm{D}} + \widehat {\rm{E}} + \widehat {\rm{F}} = 180^\circ \) (tổng ba góc trong tam giác bằng 180°)
Hay \(38^\circ + 110^\circ + \widehat {\rm{F}} = 180^\circ \)
Suy ra \(\widehat {\rm{F}} = 180^\circ - 110^\circ - 38^\circ = 32^\circ \)
Vì \(32^\circ < 38^\circ < 110^\circ \) suy ra \(\widehat {\rm{F}} < \widehat {\rm{D}} < \widehat {\rm{E}}\) (1)
Ta lại có DE; EF; DF lần lượt là các cạnh đối diện của \(\widehat {\rm{F}};{\rm{ }}\widehat {\rm{D}};{\rm{ }}\widehat {\rm{E}}\) (2)
Từ (1) và (2) suy ra DE < EF < DF (quan hệ giữa cạnh và góc trong một tam giác).
Do đó độ dài các cạnh của ∆DEF sắp xếp theo thứ tự tăng dần là: DE; EF; DF.
Vậy ta chọn phương án A.
Câu 8:
Cho ∆ABC cân tại A có BC = 9 cm; chu vi ∆ABC bằng 25 cm. Chọn khẳng định sai:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
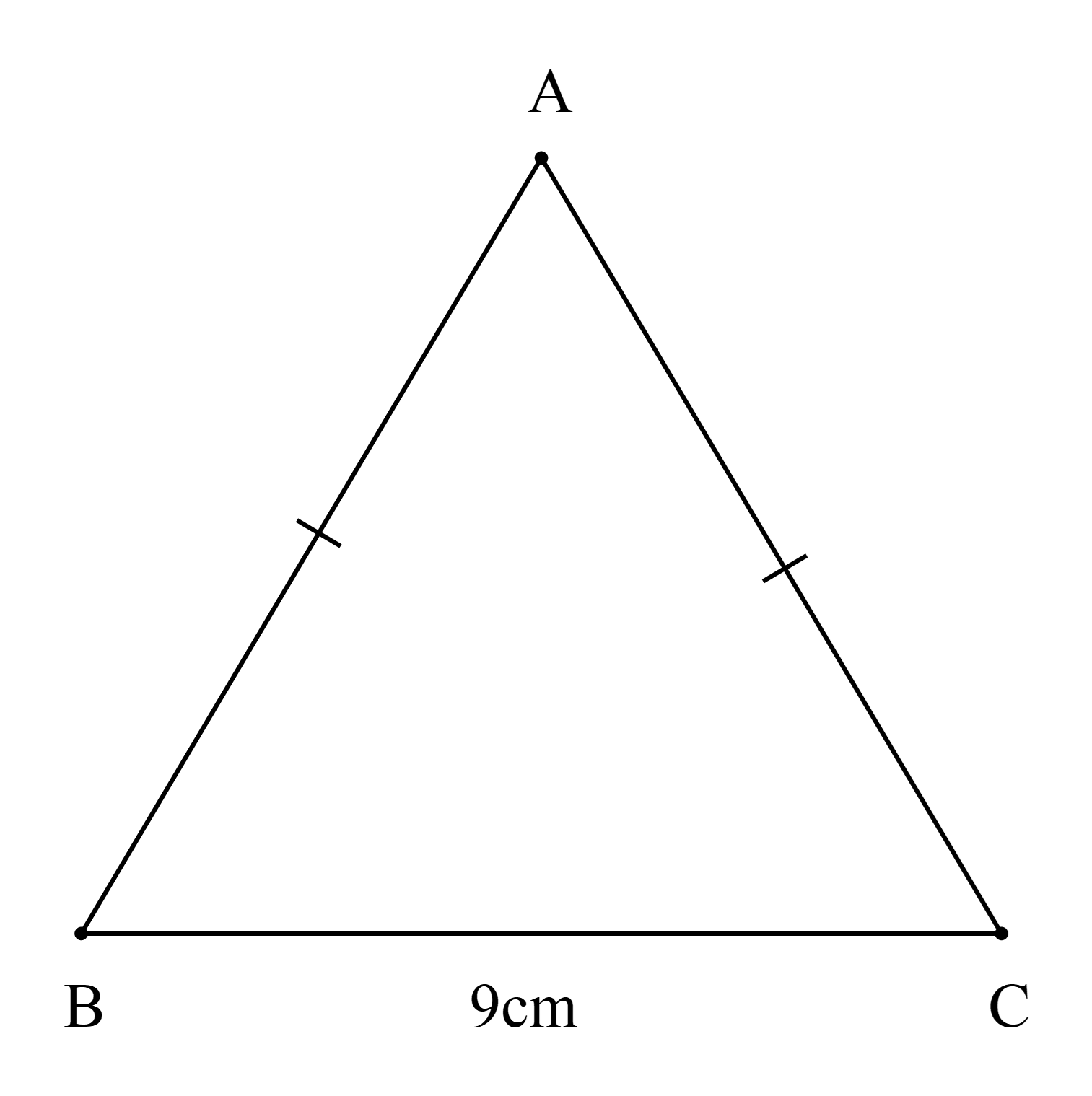
Do chu vi ∆ABC bằng 25 cm nên AB + AC + BC = 25 (cm).
Hay AB + AC + 9 = 25
Suy ra AB + AC = 25 – 9 = 16 (1)
Ta lại có AB = AC (do DABC cân tại A) (2)
Từ (1) và (2) suy ra AB = AC = \(\frac{{16}}{2} = 8\) (cm).
Ta có AB; AC; BC lần lượt là cạnh đối diện của \(\widehat {\rm{C}}{\rm{; }}\widehat {\rm{B}}{\rm{; }}\widehat {\rm{A}}\).
Mà DABC cân tại A suy ra \(\widehat {\rm{B}} = \widehat {\rm{C}}\), do đó C đúng.
AB < BC suy ra \(\widehat {\rm{C}} < \widehat {\rm{A}}\) (quan hệ giữa cạnh và góc trong tam giác), do đó D đúng, B sai
AC < BC suy ra \(\widehat {\rm{B}} < \widehat {\rm{A}}\)(quan hệ giữa cạnh và góc trong tam giác), do đó A đúng.
Vậy ta chọn phương án B.
Câu 9:
Cho góc nhọn \(\widehat {xOy}\), trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Đường trung trực của OA và đường trung trực của OB cắt nhau tại I.
Cho các khẳng định sau:
(I) OI là tia phân giác của \(\widehat {xOy}\);
(II) OI là đường trung trực của đoạn AB.
Chọn khẳng định đúng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
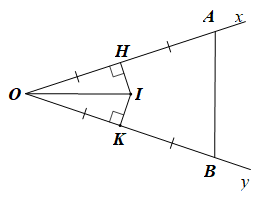
Vì HI là trung trực của OA nên IH ⊥ OA, OH = HA = \(\frac{1}{2}\)OA;
Vì KI là trung trực của OB nên IK ⊥ OB, OK = KB = \(\frac{1}{2}\)OB.
Mà OA = OB (giả thiết) nên OH = OK.
Xét DOIH và DOIK có
\(\widehat {OHI} = \widehat {OKI}( = 90^\circ )\),
OI là cạnh chung,
OH = OK (chứng minh trên)
Do đó DOIH = DOIK (cạnh huyển – cạnh góc vuông).
Suy ra \(\widehat {HOI} = \widehat {KOI}\) (hai góc tương ứng).
Do đó OI là tia phân giác của \(\widehat {xOy}\), nên (I) đúng.
Xét DOAB có IH là trung trực của OA, IK là trung trực của OB, IH cắt IK tại H nên I là giao điểm của ba đường trung trực trong tam giác OAB.
Do đó OI là trung trực của AB, nên (II) đúng.
Vậy ta chọn phương án C.
Câu 10:
Cho tam giác ABC nhọn, đường cao AH. Lấy điểm D sao cho AB là trung trực của HD. Lấy điểm E sao cho AC là trung trực của HE. Gọi M là giao điểm của DE và AB, gọi N là giao điểm của DE và AC. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
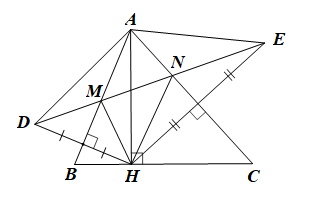
Xét DDHE có AB, AC là hai đường trung trực của tam giác cắt nhau tại A nên A cách đều ba đỉnh của tam giác
Do đó AD = AH = AE.
Tam giác ADE có AD = AE nên là tam giác cân tại A.
Suy ra \(\widehat {ADE} = \widehat {AED}\) (tính chất tam giác cân) (1)
Xét DADM và DAHM có
AM là cạnh chung,
DM = HM (do M thuộc trung trực của DH),
AD = AH (chứng minh trên).
Do đó DADM = DAHM (c.c.c).
Suy ra \(\widehat {ADM} = \widehat {AHM}\)(hai góc tương ứng) (2)
Xét DANH và DANE có
AN là cạnh chung,
NH = NE (do N thuộc trung trực của EH),
AH = AE (chứng minh trên)
Do đó DANH = DANE (c.c.c)
Suy ra \(\widehat {AHN} = \widehat {AEN}\)(hai góc tương ứng) (3)
Từ (1), (2) và (3) suy ra \(\widehat {AHN} = \widehat {AHM}\)
Do đó HA là tia phân giác của góc MHN.
Vậy ta chọn phương án C.
Câu 11:
Cho tam giác DEF có DM, EN là hai đường trung tuyến cắt nhau tại G. Kéo dài DM lấy điểm H sao cho MH = MD. Kéo dài EN lấy điểm K sao cho NK = NE. Chọn khẳng định sai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
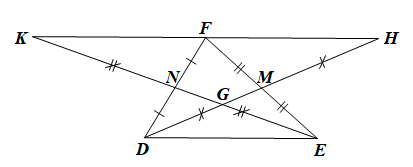
• Xét DKFN và DEDN có
NF = ND (vì N là trung điểm của DF),
\(\widehat {KNF} = \widehat {END}\) (hai góc đối đỉnh),
KN = EN (giả thiết)
Do đó DKFN = DEDN (c.g.c)
Suy ra KF = DE (hai cạnh tương ứng).
Do đó phương án A là đúng.
• Chứng minh tương tự ta cũng có: DFHM = DEDM (c.g.c)
Suy ra HF = DE (hai cạnh tương ứng).
Do đó phương án B là đúng.
• Do DFHM = DEDM (c.g.c) nên \(\widehat {MHF} = \widehat {MDE}\)(hai góc tương ứng)
Mà hai góc này ở vị trí so le trong
Suy ra FH // DE. Do đó phương án D là đúng.
Vậy ta chọn phương án C.
Câu 12:
Cho tam giác MNP có trung tuyến MA, NC cắt nhau tại O. Biết MO = 2,5 cm, OC = 1 cm. Độ dài các đường trung tuyến MA, NC lần lượt là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
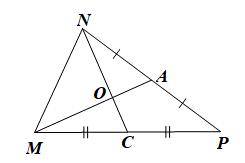
Xét DMNP có O là giao điểm của hai đường trung tuyến MA, NC nên O là trọng tâm tam giác MNP.
Suy ra NO = \(\frac{2}{3}\)NC, MO = \(\frac{2}{3}\)MA
Do đó OC = \(\frac{1}{3}\)NC hay NC = 3OC và MA = \(\frac{3}{2}\)MO.
Mà MO = 2,5 cm, OC = 1 cm (giả thiết)
Nên NC = 3 . 1 = 3 (cm), MA = \(\frac{3}{2}\). 2,5 = 3,75 (cm).
Vậy ta chọn phương án B.
Câu 13:
Cho ∆ABC vuông tại A. Trên cạnh AC lấy điểm M bất kì (M ≠ A, C). Qua M kẻ đường thẳng vuông góc với BC tại N. Từ C kẻ đường thẳng vuông góc với BM tại P. Gọi D là giao điểm của AB và CP. Khẳng định nào sau đây sai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
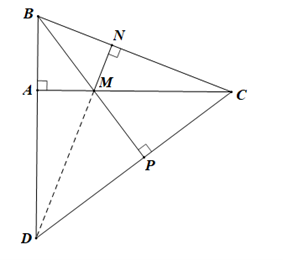
• Xét ∆DBC có CA, BP là hai đường cao cắt nhau tại M nên M là trực tâm của ∆DBC.
Do đó phương án A đúng.
• Vì M là trực tâm của ∆DBC nên DM ⊥ BC.
Do đó phương án B đúng.
• Ta có DM ⊥ BC (chứng minh trên).
Mà MN ⊥ BC (giả thiết).
Suy ra D, M, N thẳng hàng.
Do đó phương án C đúng.
• Ta có:
+) D ∈ MN (do D, M, N thẳng hàng);
+) D ∈ AB (giả thiết);
+) D ∈ CP (giả thiết).
Suy ra AB, MN, CP cùng đồng quy tại điểm D.
Do đó phương án D sai.
Vậy ta chọn phương án D.
Câu 14:
Cho tam giác AOM có \(\widehat A = 52^\circ \). Ba đường phân giác cắt nhau tại I. Số đo góc MIO là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
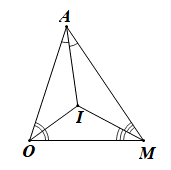
Xét DAOM ba đường phân giác cắt nhau tại I nên OI, MI lần lượt là phân giác của góc AOM, OMA.
Suy ra \(\widehat {IOM} = \widehat {IOA} = \frac{1}{2}\widehat {AOM}\),\(\widehat {IMO} = \widehat {IMA} = \frac{1}{2}\widehat {AMO}\)
Do đó \(\widehat {IMO} + \widehat {IOM} = \frac{1}{2}\left( {\widehat {AMO} + \widehat {AOM}} \right)\)
Xét DMAO có \(\widehat {AMO} + \widehat {AOM} + \widehat {OAM} = 180^\circ \) (tổng ba góc trong một tam giác)
Suy ra \(\widehat {OMA} + \widehat {AOM} = 180^\circ - \widehat {OAM} = 180^\circ - 52^\circ = 128^\circ \).
Do đó \(\widehat {IMO} + \widehat {IOM} = \frac{1}{2}\left( {\widehat {AMO} + \widehat {AOM}} \right) = \frac{1}{2}.128^\circ = 64^\circ \).
Xét DMIO có \(\widehat {IMO} + \widehat {IOM} + \widehat {MIO} = 180^\circ \) (tổng ba góc trong một tam giác)
Suy ra \(\widehat {MIO} = 180^\circ - \left( {\widehat {IMO} + \widehat {IOM}} \right) = 180^\circ - 64^\circ = 116^\circ \).
Vậy ta chọn phương án B.
Câu 15:
Cho tam giác ABC có AH, BK, CL lần lượt là ba đường cao của tam giác ABC. Chọn khẳng định đúng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B

+) Ta có AH là đường vuông góc và AB là các đường xiên kẻ từ A đến BC.
Do đó AH < AB (1)
+) Ta có BK là đường vuông góc và BC là các đường xiên kẻ từ B tới AC.
Do đó BK < BC (2)
+) Ta có CL là đường vuông góc và CA là các đường xiên kẻ từ B tới AB.
Do đó CL < CA (3)
Từ (1) (2) và (3) suy ra:
AH + BK + CL < AB + BC + CA.
Vậy ta chọn phương án B.
