Cho nhọn, các đường cao AH, BD và CE . Gọi M,N ,P , Q thứ tự là hình chiếu của H trên AB,BD , CE và AC. Chứng minh M,N ,P , Q thẳng hàng.
 Giải bởi Vietjack
Giải bởi Vietjack
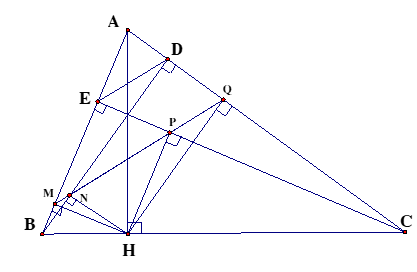
+ Từ (gt) ; (định lý Talét).
(định ký Talét đảo) .
+ Chứng minh tương tự ta có:
+ Áp dụng hệ thức lượng trong tam giác vuông và ta có:
mà (vì (g.g)).
hay . (định lý Talét đảo)
Kết hợp với (1), (2) ta có:
M,N ,Q thẳng hàng và M, P , Q thẳng hàng (tiên đề Ơclít).
Do đó M , N, P, Q thẳng hàng.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hình chữ nhật ABCD có O là giao điểm 2 đường chéo. Điểm M trên đoạn OB, lấy E đối xứng với A qua M; H là hình chiếu của điểm E trên BC, vẽ hình chữ nhật EHCF. Chứng minh M, H, F thẳng hàng.
Cho đường tròn (O; R) và một điểm A nằm ngoài đường tròn (O) sao cho OA=2R. Từ A vẽ tiếp tuyến AB của đường tròn (O) (B là tiếp điểm).
1) Chứng minh tam giác ABO vuông tại B và tính độ dài AB theo R
2) Từ B vẽ dây cung BC của (O) vuông góc với cạnh OA tại H. Chứng minh AC là tiếp tuyến của đường tròn (O).
4) Từ H vẽ đường thẳng vuông góc với AB tại D. Đường tròn đường kính AC cắt cạnh DC tại E. Gọi F là trung điểm của cạnh OB. Chứng minh ba điểm A, E, F thẳng hàng.