Cho tam giác ABC có là góc tù , điểm D di chuyển trên cạnh BC . Xác định vị trí của điểm D sao cho tổng các khoảng cách từ B và C đến đường thẳng AD có giá trị lớn nhất .
 Giải bởi Vietjack
Giải bởi Vietjack
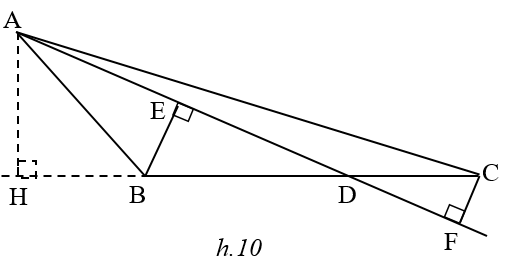
Gọi S là diện tích DABC Khi D di chuyển trên cạnh BC ta có :
SABD + SACD = S
Kẻ BE vuông góc AD , CF vuông góc AD
AD.BE +AD.CF = S
BE +CF =
Do đó BE + CF lớn nhất AD nhỏ nhất hình chiếu HD nhỏ nhất
Do HD ≥ HB ( do >900 ) và HD = HB D ≡ B
Vậy Khi D ≡ B thì tổng các khoảng cách từ B và C đến AD có giá trị lớn nhất .
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho đoạn thẳng AB có độ dài 2a .Vẽ về một phía của AB các tia Ax và By vuông góc với AB. Qua trung điểm của M của AB có hai đường thẳng thay đổi luôn vuông góc với nhau và cắt Ax, By theo thứ tự tại C và D. Xác định vị trí của các điểm C,D sao cho tam giác MCD có diện tích nhỏ nhất . Tính diện tích tam giác đó.
Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA ta lấy theo thứ tự các điểm E,F,G,H sao cho AE = BF = CG = DH . Xác định vị trí của các điểm E, F,G,H sao cho tứ giác EFGH có chu vi nhỏ nhất .
Trong các hình bình hành có hai đường chéo bằng 6 cm và 8 cm, hình nào có diện tích lớn nhất? Tính diện tích lớn nhất đó.