Cho điểm M nằm trên đoạn thẳng AB .Vẽ về một phía của AB các tia Ax và By vuông góc với AB . Qua M có hai đường thẳng thay đổi luôn vuông góc với nhau và cắt Ax, By theo thứ tự tại C và D . Xác định vị trí của các điểm C,D sao cho tam giác MCD có diện tích nhỏ nhất .
 Giải bởi Vietjack
Giải bởi Vietjack
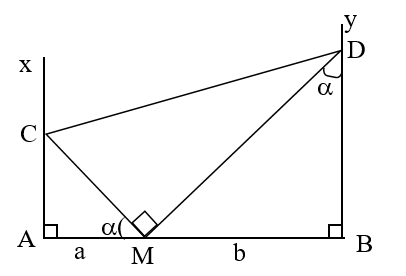
Ta có : SMCD = MC.MD
Đặt MA = a , MB = b
MC = , MD =
SMCD =
Do a,b là hằng số nên SMCD nhỏ nhất 2sina.cosa lớn nhất .
Theo bất đẳng thức 2xy x2 +y2 ta có :
2sina.cosa sin2a +cos2a = 1 nên SMCD ≥ ab
SMCD = ab sina = cosa sina = sin(900-a) a = 900-a a = 450
Tam giác AMC và tam giác BMD vuông cân.
Vậy min SMCD = ab. Khi đó các điểm C,D được xác định trên tia Ax ; By sao cho AC = AM , BD = BMGói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC vuông cân có cạnh huyền BC = a . Gọi D là trung điểm của AB. Điểm E di chuyển trên cạnh AC. Gọi H,K theo thứ tự là chân các đường vuông góc kẻ từ D, E đến BC . Tính diện tích lớn nhất của hình thang DEKH . Khi đó hình thang trở thành hình gì ?
Cho tam giác ABC , điểm M di động trên cạnh BC . Qua M kẻ các đường thẳng song song với AC và với AB , chúng cắt AB và AC theo thứ tự ở D và E.Xác định vị trí của điểm M sao cho hình bình hành ADME có diện tích lớn nhất.
Cho đoạn thẳng AB, điểm M di chuyển trên đoạn thẳng ấy . Vẽ các đường tròn có đường kính MA và MB . Xác định vị trí của điểm M để tổng diện tích của hai hình tròn có giá trị nhỏ nhất .