Cho tam giác có một đường phân giác đồng thời là đường trung trực ứng với cùng một cạnh thì tam giác đó là tam giác
A. Tam giác vuông;
B. Tam giác cân;
C. Tam giác nhọn;
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
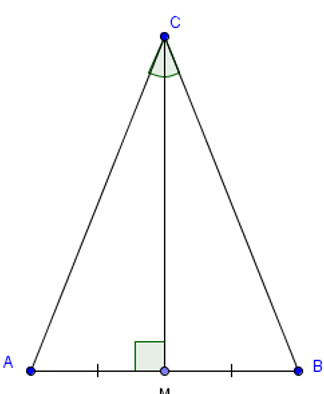
Giả sử tam giác ABC có đường phân giác CM. Khi đó CM cũng là đường trung trực của AB.
Vì CM là đường phân giác nên
Vì CM là đường trung trực của AB nên
Xét ∆AMC và ∆BMC có
CM là cạnh chung
Suy ra ∆AMC = ∆BMC (g.c.g)
Do đó CA = CB (hai cạnh tương ứng)
Suy ra tam giác ABC cân tại C
Hay tam giác có một đường phân giác đồng thời là đường trung trực ứng với cùng một cạnh thì tam giác đó là tam giác cân.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong ∆ABC hai đường trung trực của hai cạnh AB và AC cắt nhau tại D nằm trên cạnh C. Khẳng định đúng nhất là
Cho ∆ABC cân tại A, trung tuyến AM, đường trung trực của AC cắt AM ở D. Khẳng định đúng là
Cho tam giác ABC cân tại A có góc A bằng 40°. Đường trung trực của AB cắt AB tại H, cắt BC tại D. Số đo góc ADB là
Cho ∆MAB, ∆NAB, ∆PAB là ba tam giác cân chung đáy AB. Khẳng định đúng là
Đường trung trực của đoạn AB cắt AB tại H. Hai điểm M, N là hai điểm trên đường trung trực đó (N nằm giữa M và H). Gọi N’ là giao điểm của AN và BM. Khẳng định sai là
