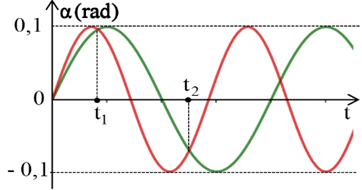
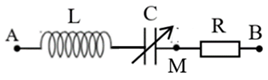Hai con lắc đơn có chiều dài \[{\ell _1} = \,100\,{\rm{cm}}\] và \[{\ell _2}\] (với \[{\ell _2} < {\ell _1})\] được treo tại cùng một nơi có \[{\rm{g = 10}}\,{\rm{m/}}{{\rm{s}}^{\rm{2}}}.\]Bỏ qua lực cản không khí, lấy \[{{\rm{\pi }}^{\rm{2}}} = 10.\] Ban đầu, từ vị trí cân bằng đồng thời truyền vận tốc ban đầu nằm ngang, cùng chiều cho mỗi con lắc sao cho chúng dao động điều hòa cùng trong hai mặt phẳng song song với nhau. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của li độ góc của mỗi con lắc theo thời gian. Biết \[{{\rm{t}}_{\rm{2}}}{\rm{ - }}{{\rm{t}}_{\rm{1}}}{\rm{ = }}\frac{{\rm{8}}}{{\rm{9}}}\,{\rm{s}}{\rm{.}}\] Không kể lúc truyền vận tốc, tại thời điểm mà hai dây treo song song với nhau lần thứ 2023 thì tốc độ của con lắc có chiều dài \[{\ell _2}\]là
D. \[14,0\,{\rm{cm/s}}{\rm{.}}\]
Giải bởi Vietjack
\({\omega _1} = \sqrt {\frac{g}{{{l_1}}}} \approx \sqrt {\frac{{{\pi ^2}}}{1}} = \pi \) (rad/s) \( \Rightarrow {T_1} = \frac{{2\pi }}{{{\omega _1}}} = 2s\) và \({l_2} < {l_1} \Rightarrow {\omega _2} > {\omega _1}\)
(chú ý nghiệm \({\omega _2}t = {\omega _1}t + k2\pi \) là cùng chiều, còn nghiệm \({\omega _2}t = \pi - {\omega _1}t + h2\pi \) là ngược chiều)
(rad/s) \( \Rightarrow \left\{ \begin{array}{l}{T_2} = \frac{{2\pi }}{{{\omega _2}}} = 1,6s\\{l_2} = \frac{g}{{\omega _2^2}} = 0,64m\end{array} \right.\)
\(\frac{{{T_1}}}{{{T_2}}} = \frac{2}{{1,6}} = \frac{5}{4} \Rightarrow {T_{12}} = 8s\) thì 2 vật lặp lại trạng thái ban đầu nên ta chỉ cần xét trong 8s đầu
Từ cứ \({T_{12}} = 8s\) thì có 10 lần
\(2013 = 201.10 + 3 \Rightarrow {t_3} = \frac{4}{9} + \frac{{8.2}}{9} = \frac{{20}}{9}s\)
\({s_2} = {l_2}{\alpha _2} = {l_2}{\alpha _0}\sin \left( {{\omega _2}t} \right) \Rightarrow {v_2} = {s_2}' = {l_2}{\alpha _0}{\omega _2}\cos \left( {{\omega _2}t} \right) = 0,64.0,1.\frac{{5\pi }}{4}.\cos \left( {\frac{{5\pi }}{4}.\frac{{20}}{9}} \right) \approx - 0,193m/s\)Vậy \(\left| {{v_2}} \right| \approx 19,3cm/s\). Chọn A
Cách 2:
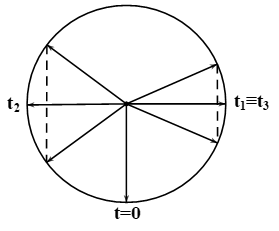
\({\omega _1} = \sqrt {\frac{g}{{{l_1}}}} \approx \sqrt {\frac{{{\pi ^2}}}{1}} = \pi \) (rad/s) \( \Rightarrow {T_1} = \frac{{2\pi }}{{{\omega _1}}} = 2s\)
Tạo dao động ảo có tần số góc \(\omega = \frac{{{\omega _1} + {\omega _2}}}{2} \Rightarrow \)pha dao động cũng bằng trung bình cộng
\( \Rightarrow {t_2} - {t_1} = \frac{T}{2} = \frac{8}{9}s \Rightarrow T = \frac{{16}}{9}s \Rightarrow \omega = \frac{{2\pi }}{T} = \frac{{9\pi }}{8} = \frac{{\pi + {\omega _2}}}{2} \Rightarrow {\omega _2} = \frac{{5\pi }}{4}(rad/s) \Rightarrow \left\{ \begin{array}{l}{T_2} = \frac{{2\pi }}{{{\omega _2}}} = 1,6s\\{l_2} = \frac{g}{{\omega _2^2}} = 0,64m\end{array} \right.\)\(\frac{{{T_1}}}{{{T_2}}} = \frac{2}{{1,6}} = \frac{5}{4} \Rightarrow \) cứ \({T_{12}} = 8s\) thì hơn nhau 1 dao động nên cứ sau \(8s\) mới có 1 lần 2 dao động cùng pha mà \({T_{12}} = 8s = \frac{T}{4} + 8,5.\frac{T}{2} \Rightarrow \)có 9 lần dao động ảo đi qua biên + 1 lần cùng pha: 10 lần
\(2013 = 201.10 + 3 \Rightarrow {t_3} = \frac{T}{4} + 2.\frac{T}{2} = \frac{{20}}{9}s\)
\({s_2} = {l_2}{\alpha _2} = {l_2}{\alpha _0}\cos \left( {{\omega _2}t - \frac{\pi }{2}} \right) \Rightarrow {v_2} = {l_2}{\alpha _0}{\omega _2}\cos \left( {{\omega _2}t} \right) = 0,64.0,1.\frac{{5\pi }}{4}.\cos \left( {\frac{{5\pi }}{4}.\frac{{20}}{9}} \right) \approx - 0,193m/s\)Vậy \(\left| {{v_2}} \right| \approx 19,3cm/s\). Chọn A
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Đặt điện áp \[{{\rm{u}}_{{\rm{AB}}}}{\rm{ = 60}}\sqrt {\rm{2}} {\rm{cos100\pi t}}\,{\rm{(V)}}\,\]vào hai đầu đoạn mạch AB như hình bên, trong đó cuộn thuần cảm có độ tự cảm L, tụ điện có điện dung C thay đổi được. Khi \[{\rm{C = }}{{\rm{C}}_{\rm{0}}}\] thì điện áp hiệu dụng giữa hai đầu đoạn MN đạt cực đại và điện áp hiệu dụng giữa hai đầu đoạn AN là 120 V. Khi \[{\rm{C = 0,5}}{{\rm{C}}_{\rm{0}}}\] thì biểu thức điện áp tức thời giữa hai đầu cuộn cảm là
Sóng điện từ hình sin lan truyền trong không gian. Tại một điểm M có sóng truyền tới, cường độ điện trường và cảm ứng từ tại đó biến thiên cùng tần số và
Đặt điện áp \[{\rm{u = }}{{\rm{U}}_{\rm{0}}}{\rm{cos}}\left( {{\rm{\omega t + \varphi }}} \right)\]vào hai đầu đoạn mạch R, L, C mắc nối tiếp thì trong mạch có hiện tượng cộng hưởng điện. Hệ thức nào sau đây là đúng?
Đặt điện áp xoay chiều vào hai đầu đoạn mạch R, L, C mắc nối tiếp thì cảm kháng, dung kháng của cuộn cảm và của tụ điện lần lượt là \[{{\rm{Z}}_{\rm{L}}}{\rm{;}}\,{{\rm{Z}}_{\rm{C}}}{\rm{.}}\]Hệ số công suất của đoạn mạch là
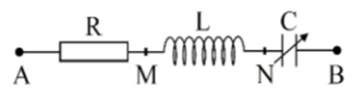
Đặt điện áp \[{\rm{u = }}\,{{\rm{U}}_{\rm{0}}}{\rm{cos}}\left( {{\rm{\omega t + \varphi }}} \right)\](trong đó \[{{\rm{U}}_{\rm{0}}}{\rm{;}}\,{\rm{\omega ;}}\,{\rm{\varphi }}\]không đổi) vào hai đầu đoạn mạch như hình bên. Cuộn dây thuần cảm có độ tự cảm không đổi, điện trở có giá trị không đổi, tụ điện có điện dung thay đổi được. Khi điện dung của tụ điện là C = C1 thì điện áp tức thời giữa hai điểm A, M có biểu thức \[{{\rm{u}}_{{\rm{AM}}}}{\rm{ = }}{{\rm{U}}_{{\rm{01}}}}{\rm{cos}}\left( {{\rm{\omega t + }}\frac{{\rm{\pi }}}{{\rm{3}}}} \right).\] Khi điện dung của tụ điện là C = C2 thì điện áp tức thời giữa hai điểm A, M có biểu thức \[{{\rm{u}}_{{\rm{AM}}}}{\rm{ = 0,75}}{\rm{.}}{{\rm{U}}_{{\rm{01}}}}{\rm{cos}}\left( {{\rm{\omega t - }}\frac{{\rm{\pi }}}{{\rm{6}}}} \right).\] Khi C = C1 thì hệ số công suất của đoạn mạch AB là
Một vật có khối lượng m = 100 g, dao động điều hòa trên trục Ox theo phương trình \[{\rm{x = 6}}{\rm{.cos}}\left( {{\rm{10t + 0,5\pi }}} \right)\,{\rm{cm}}\](với t tính bằng s). Mốc thế năng tại vị trí cân bằng. Cơ năng của vật là
Một con lắc lò xo có độ cứng k, vật nhỏ có khối lượng m dao động điều hòa. Chu kì dao động của con lắc là
Hạt nhân \[{}_{\rm{Z}}^{\rm{A}}{\rm{X}}\] có khối lượng m, khối lượng của prôton là mp; của nơtron là mn. Độ hụt khối của X là
Phản ứng hạt nhân \[{}_{\rm{1}}^{\rm{2}}{\rm{H + }}{}_{\rm{1}}^{\rm{3}}{\rm{H}} \to {}_{\rm{2}}^{\rm{4}}{\rm{He + }}{}_{\rm{0}}^{\rm{1}}{\rm{n + 17,6}}\,{\rm{MeV}}\] là phản ứng
Câu chuyện về một giọng hát ôpêra cao và khỏe có thể làm vỡ cái cốc uống rượu để gần là do liên quan đến
Xét phân hạch của hạt nhân \[{}_{{\rm{92}}}^{{\rm{235}}}{\rm{U,}}\] sau mỗi phân hạch có k nơtron được giải phóng đến kích thích các hạt nhân khác. Để phản ứng dây chuyền xảy ra dưới dạng kiểm soát được thì giá trị của k là
