Tính biệt thức từ đó tìm số nghiệm của phương trình 9x2 − 15x + 3 = 0
A. = 117 và phương trình có nghiệm kép
B. = − 117 và phương trình vô nghiệm
C. = 117 và phương trình có hai nghiệm phân biệt
D. = − 117 và phương trình có hai nghiệm phân biệt
 Giải bởi Vietjack
Giải bởi Vietjack
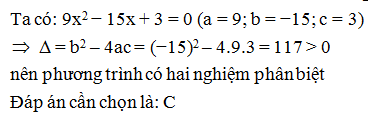
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tính biệt thức từ đó tìm các nghiệm (nếu có) của phương trình x2 − x − 1 = 0
Tính biệt thức từ đó tìm các nghiệm (nếu có) của phương trình x2 − 2x + 2 = 0
Không dùng công thức nghiệm, tính tổng các nghiệm của phương trình 6x2 – 7x = 0
Không dùng công thức nghiệm, tìm số nghiệm của phương trình −4x2 + 9 = 0
Cho phương trình x2 – (m – 1)x − m = 0. Kết luận nào sau đây là đúng?
Tính biệt thức từ đó tìm số nghiệm của phương trình −13x2 + 22x − 13 = 0
Tìm tích các giá trị của m để phương trình 4mx2 − x – 14m2 = 0 có nghiệm x = 2
Cho phương trình 2x2 + (2m – 1)x + m2 – 2m + 5 = 0. Kết luận nào sau đây là đúng?
Tìm tổng các giá trị của m để phương trình (m – 2)x2 – (m2 + 1)x + 3m = 0 có nghiệm x = −3
1. Định nghĩa
Định nghĩa: Phương trình bậc hai một ẩn (nói gọn là phương trình bậc hai) là phương trình có dạng
![]()
trong đó x là ẩn, a, b, c là những số cho trước gọi là các hệ số và .
Ví dụ 1:
a) là một phương trình bậc hai với a = 1; b = -2; c = 1.
b) là một phương trình bậc hai với a = 1; b = 0; c = -9.
2. Một số ví dụ về giải phương trình bậc hai
a) Trường hợp b = 0.
Với trường hợp b = 0 thì khi đó phương trình bậc hai của chúng ta là
+ Nếu a và c cùng dấu thì phương trình sẽ vô nghiệm
Ví dụ 2: (vô lí)
+ Nếu a và c trái dấu thì phương trình sẽ có hai nghiệm
Ví dụ 3: .
b) Trường hợp c = 0.
Với trường hợp c = 0 thì khi đó phương trình bậc hai của chúng ta là
Khi đó phương trình luôn có hai nghiệm là x = 0 và .
Ví dụ 4:
c) Trường hợp .
Khi đó ta sẽ biến đổi phương trình thành tổng của một bình phương với một số.
Ví dụ 5: