Có bao nhiêu số nguyên x để giá trị của đa thức A = 2x3 – 3x2 + 2x + 2 chia hết cho giá trị của đa thức B = x2 + 1
A. 3
B. 4
C. 2
D. 1
 Giải bởi Vietjack
Giải bởi Vietjack
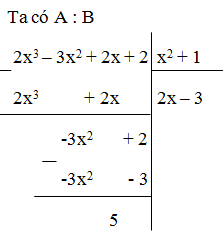
Để giá trị của đa thức A = 2x3 – 3x2 + 2x + 2 chia hết cho giá trị của đa thức B = x2 + 1 thì 5 chia hết (x2 + 1)
Hay (x2 + 1) U(5) = {-1; 1; -5; 5}
+) x2 + 1 = -1 x2 = -2 (VL)
+) x2 + 1 = 1 x2 = 0 x = 0 (tm)
+) x2 + 1 = -5 x2 = -6 (VL)
+) x2 + 1 = 5 x2 = 4 x = ± 2 (tm)
Vậy có 3 giá trị của x thỏa mãn đề bài là x = 0; x = -2; x = 2
Đáp án cần chọn là: A
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tìm giá trị của a và b để đa thức 4x3 + ax + b chia cho đa thức x2 – 1 dư 2x – 3.
Cho đa thức f(x) = x4 – 3x3 + 3x2 + ax + b và đa thức g(x) = x2 – 3x + 4. Biết f(x) chia hết cho g(x). Khi đó tích a.b bằng
Biết đa thức x4 + ax2 + b chia hết cho x2 – x + 1. Khi đó, khẳng định nào sau đây là đúng
Tìm a và b để đa thức f(x) = x4 – 9x3 + 21x2 + ax + b chia hết cho đa thức g(x) = x2 – x – 2
Tìm các hằng số a và b sao cho (x3 + ax + b) : (x + 1) dư 7 và (x3 + ax + b) : (x – 3) dư (-5)
Xác định hằng số a và b sao cho (x4 + ax + b) chia hết (x2 – 4)
Phần dư của phép chia đa thức (x2 + 3x + 2)5 + (x2 – 4x – 4)5 – 1 cho đa thức x + 1 là
1. Phép chia hết:
- Phép chia hết là phép chia có đa thức dư bằng 0.
Quy tắc chia:
+ Sắp xếp các đa thức theo thứ tự giảm dần của biến.
+ Lấy hạng tử cao nhất của đa thức bị chia chia cho hạng tử cao nhất của đa thức chia ta được thương 1.
+ Nhân thương 1 với đa thức chia và lấy đa thức bị chia trừ đi tích đó.
+ Lấy hạng tử cao nhất của đa thức vừa tìm được chia cho hạng tử cao nhất đa thức chia ta được thương 2.
+ Tiếp tục lặp lại các bước trên đến khi nhận được hiệu bằng 0.
Ví dụ 1: Làm tính chia:
Lời giải:
Ta có:
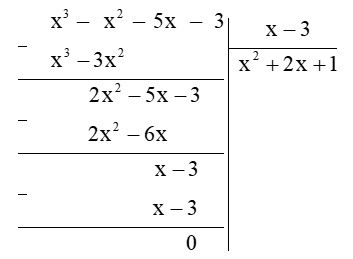
Vậy .
2. Phép chia có dư:
- Phép chia có dư là phép chia có đa thức dư khác 0.
Quy tắc chia: Làm tương tự phép chia hết đến khi thu được đa thức dư có bậc nhỏ hơn bậc của đa thức chia.
Chú ý: Với hai đa thức tùy ý A và B của cùng một biến (B ≠ 0), tồn tại duy nhất một cặp đa thức Q và R sao cho A = B.Q + R, trong đó R = 0 hoặc bậc của R nhỏ hơn bậc của B (R được gọi là dư trong phép chia A cho B).
Khi R = 0 phép chia A cho B là phép chia hết.
Ví dụ 2: Làm tính chia: .
Lời giải:
Ta có:
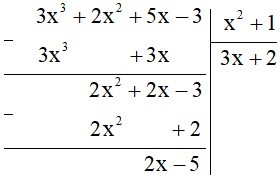
Vậy
Hay .