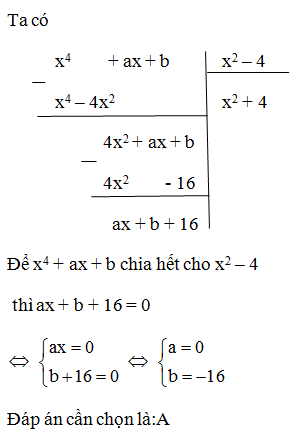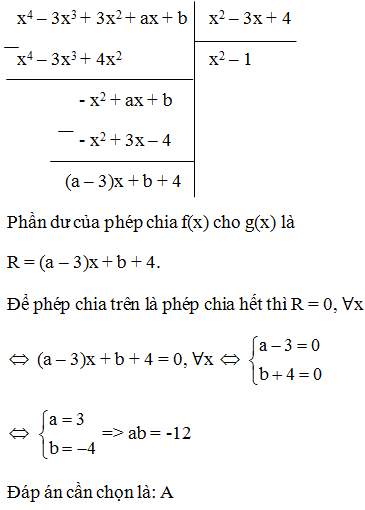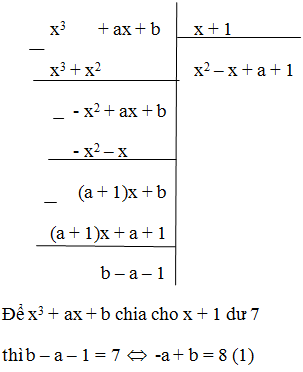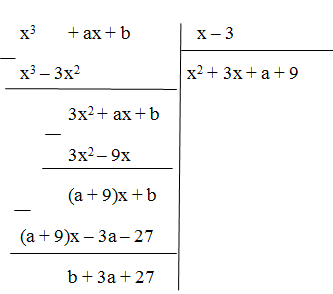Trắc nghiệm Chia đa thức một biến đã sắp xếp có đáp án (Vận dụng)
-
1603 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tìm giá trị của a và b để đa thức 4x3 + ax + b chia cho đa thức x2 – 1 dư 2x – 3.
Xem đáp án
Ta có
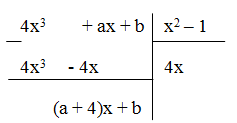
Phần dư của phép chia trên là R = (a + 4)x + b
Theo bài ra ta có (a + 4)x + b = 2x – 3 <=> <=>
Vậy có hai giá trị của a thỏa mãn điều kiện đề bài a = -2; b = -3
Đáp án cần chọn là: D
Câu 2:
Tìm a và b để đa thức f(x) = x4 – 9x3 + 21x2 + ax + b chia hết cho đa thức g(x) = x2 – x – 2
Xem đáp án
Ta có:
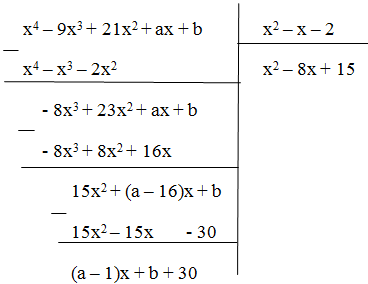
Phần dư của phép chia f(x) cho g(x) là R = (a – 1)x + b + 30
Để phép chia trên là phép chia hết thì R = 0 với mọi x
(a – 1)x + b + 30 = 0 với mọi x
<=> <=>
Vậy a = 1; b = -30
Đáp án cần chọn là: D
Câu 4:
Biết đa thức x4 + ax2 + b chia hết cho x2 – x + 1. Khi đó, khẳng định nào sau đây là đúng
Xem đáp án
Ta có :
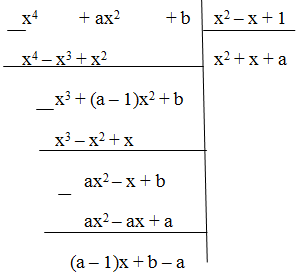
Phần dư của phép chia là R = (a – 1)x + b – a. Để phép chia trên là phép chia hết thì R = 0,
(a – 1)x + b – a = 0
<=> <=> a = b
Đáp án cần chọn là: C
Câu 6:
Xác định a để (6x3 – 7x2 – x + a) : (2x + 1) dư 2
Xem đáp án
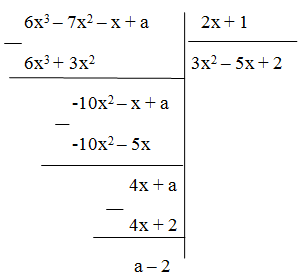
Để 6x3 – 7x2 – x + a chia 2x + 1 dư 2 thì a – 2 = 2 Vậy a = 4
Đáp án cần chọn là: D
Câu 9:
Có bao nhiêu số nguyên x để giá trị của đa thức A = 2x3 – 3x2 + 2x + 2 chia hết cho giá trị của đa thức B = x2 + 1
Xem đáp án
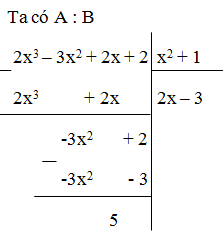
Để giá trị của đa thức A = 2x3 – 3x2 + 2x + 2 chia hết cho giá trị của đa thức B = x2 + 1 thì 5 chia hết (x2 + 1)
Hay (x2 + 1) U(5) = {-1; 1; -5; 5}
+) x2 + 1 = -1 x2 = -2 (VL)
+) x2 + 1 = 1 x2 = 0 x = 0 (tm)
+) x2 + 1 = -5 x2 = -6 (VL)
+) x2 + 1 = 5 x2 = 4 x = ± 2 (tm)
Vậy có 3 giá trị của x thỏa mãn đề bài là x = 0; x = -2; x = 2
Đáp án cần chọn là: A
Câu 10:
Phần dư của phép chia đa thức (x2 + 3x + 2)5 + (x2 – 4x – 4)5 – 1 cho đa thức x + 1 là
Xem đáp án
Ta có đa thức chia (x + 1) nên phần dư là một hằng số
Gọi thương là Q(x) và dư r. Khi đó với mọi x ta có
(x2 + 3x + 2)5 + (x2 – 4x – 4)5 – 1 = Q(x)(x + 1) + r (1)
Thay x = -1 vào (1) ta được
((-1)2 + 3.(-1) + 2)5 + ((-1)2 – 4(-1) – 4)5 – 1 = Q(x).(-1 + 1) + r
r = 05 + 15 – 1 r = 0
Vậy phần dư của phép chia là r = 0
Đáp án cần chọn là: C