Tính độ dài đường cao của hình chóp tứ giác đều với các kích thước cho trên hình 125.
 Giải bởi Vietjack
Giải bởi Vietjack
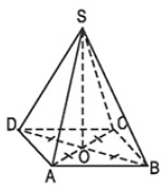
Gọi O là giao điểm của AC và BD.
Áp dụng định lí Py – ta - go vào tam giác ABC ta được
AC2 = AB2 + BC2 = 52 + 52 = 50
⇒ AC = 5√2 cm
Do O là trung điểm của AC nên: AO = OC = 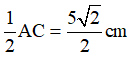
Tam giác SAO vuông tại O nên:
SA2 = SO2 – OA2
⇒ SO2 = SA2 – AO2
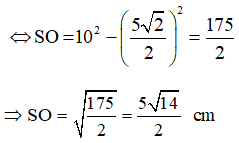
Vậy độ dài đường cao của hình chóp là 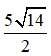 .
.
Kiến thức áp dụng
Chân đường cao của hình chóp đều là tâm của đường tròn đi qua các đỉnh của mặt đáy.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Một hình chóp tứ giác đều có độ dài cạnh bên bằng 25cm, đáy là hình vuông ABCD cạnh 30cm. Tính diện tích toàn phần của hình chóp.
Tính diện tích xung quanh, diện tích toàn phần của các hình chóp tứ giác đều sau đây (h.126).
Vẽ, cắt và gấp miếng bìa như hình đã chỉ ra ở hình 125 để được hình chóp tứ giác đều.
a) Trong hình 125a, có bao nhiêu tam giác cân bằng nhau?
b) Sử dụng định lí Pitago để tính chiều cao ứng với đáy của mỗi tam giác.
c) Diện tích xung quanh và diện tích toàn phần của hình chóp đều này là bao nhiêu?
Vẽ, cắt và gấp miếng bìa như ở hình 123. Quan sát hình gấp được, hãy điền số thích hợp vào chỗ trống (…) ở các câu dưới đây:
a) Số các mặt bằng nhau trong một hình chóp tứ giác đều là …
b) Diện tích mỗi mặt tam giác là … cm2.
c) Diện tích đáy của hình chóp đều là … cm2.
d) Tổng diện tích tất cả các mặt bên của hình chóp đều là … cm2.