Cho đường tròn (O), đường kính AB = 14cm, dây CD có độ dài 12cm vuông góc với AB tại H nằm giữa O và B. Độ dài HA là?
A. 7 + cm
B. 7 − cm
C. 7cm
D. 7 − 2cm
 Giải bởi Vietjack
Giải bởi Vietjack
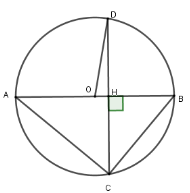
Xét (O) có AB CD tại H và AB là đường kính nên H là trung điểm của CD
HD = HC = = 6cm
Vì AB = 14 OA = OB = OD = = 7cm
Áp dụng định lý Pytago cho tam giác vuông OHD ta được:
OH =
Khi đó HA = OA + OH = 7 + cm
Đáp án cần chọn là: A
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho đường tròn (O), đường kính AB. Kẻ hai dây AC và BD song song. So sánh độ dài AC và BD
Cho đường tròn (O; R) có hai dây AB, CD bằng nhau và vuông góc với nhau tại I. Giả sử IA = 6cm; IB = 3cm. Tổng khoảng cách từ tâm O đến dây AB, CD là:
Cho đường tròn (O) và một dây CD. Từ O kẻ tia vuông góc với CD tại M, cắt (O; R) tại H. Biết CD = 16cm, MH = 4cm. Bán kính R bằng:
Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau ở M. Biết AB = 10cm; CD = 8cm; MC = 1cm. Bán kinh R và khoảng cách từ tâm O đến dây CD lần lượt là:
Cho đường tròn (O; R) có hai dây AB, CD bằng nhau và vuông góc với nhau tại I. Giả sử IA = 2cm; IB = 4cm. Tổng khoảng cách từ tâm O đến dây AB, CD là:
Cho nửa đường tròn (O), đường kính AB và một dây MN. Kẻ AE và BF vuông góc với MN lần lượt tại E và F. So sánh độ dài OE và OF.
Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau ở M. Biết AB = 16cm; CD = 12cm; MC = 2cm. Khoảng cách từ tâm O đến dây AB là?
Cho đường tròn (O; 8cm). Dây AB và CD song song, có độ dài lần lượt là 14cm và 10cm. Tính khoảng cách giữa 2 dây.
Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau ở M. Biết CD = 8cm; MC = 1cm. Khoảng cách từ tâm O đến dây AB là?
Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau ở M. Biết AB = 14cm; CD = 12cm; MC = 2cm. Bán kinh R và khoảng cách từ tâm O đến dây CD lần lượt là:
Cho đường tròn (O), đường kính AB = 20cm, dây CD có độ dài 16cm vuông góc với AB tại H nằm giữa O và B. Độ dài HA là?
Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của AB, BC. Gọi E là giao điểm của CM và DN. So sánh AE và DM
Cho nửa đường tròn (O), đường kính AB và một dây CD. Kẻ AE và BF vuông góc với CD lần lượt tại E và F. So sánh độ dài CE và DF
Cho đường tròn (O; 10cm). Dây AB và CD song song, có độ dài lần lượt là 16cm và 12cm. Tính khoảng cách giữa 2 dây.
Cho đường tròn (O; R). Hai dây AB, CD song song với nhau sao cho tâm O nằm trong dải song song tạo bởi AB, CD. Biết khoảng cách giữa hai dây đó bằng 11cm và AB = 10cm, CD = 16cm. Tính R
1. So sánh độ dài của đường kính và dây
Định lí 1. Trong các dây của một đường tròn, dây lớn nhất là đường kính.
Ví dụ 1. Gọi AB là một dây bất kỳ của đường tròn (O; R).
Chứng minh rằng AB ≤ 2R.
Lời giải:
* Trường hợp 1: AB là đường kính.
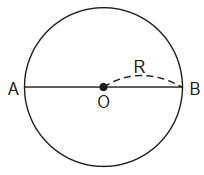
Khi đó, AB = 2R (1)
* Trường hợp 2: AB không là đường kính.
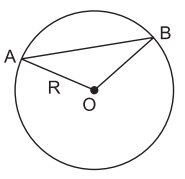
Áp dụng bất đẳng thức tam giác vào ∆AOB, ta có:
AB < AO + OB = R + R = 2R (2)
Từ (1) và (2) suy ra AB ≤ 2R (đpcm).
2. Quan hệ vuông góc giữa đường kính và dây
Định lí 2. Trong một đường tròn, đường kính vuông góc với dây thì đi qua trung điểm của dây đó.
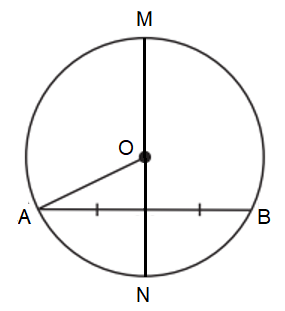
Ví dụ 2. Cho đường tròn (O) đường kính AB. Dây CD của đường tròn (O). Biết tại I.
Khi đó, IC = ID (như hình vẽ).
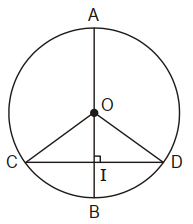
Định lí 3. Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.
Ví dụ 3. Cho đường tròn (O) đường kính MN và dây AB. Đường kính MN đi qua trung điểm của dây AB.
Khi đó (như hình vẽ).