18 câu hỏi trắc nghiệm thuộc Trắc nghiệm Đường kính và dây của đường tròn có đáp án (Vận dụng)

Câu 1:

Cho đường tròn (O; R) có hai dây AB, CD bằng nhau và vuông góc với nhau tại I. Giả sử IA = 2cm; IB = 4cm. Tổng khoảng cách từ tâm O đến dây AB, CD là:

A. 4cm

B. 1cm

C. 3cm

D. 2cm

Xem đáp án

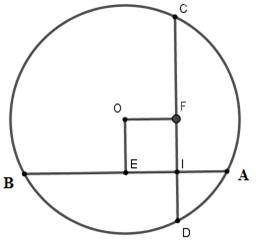
Xét đường tròn tâm (O).

Kẻ OEAB tại E suy ra E là trung điểm của AB, kẻ OFCD tại F.

Vì dây AB = AC nên OE = OF (hai dây bằng nhau cách đều tâm)

Xét tứ giác OEIF có = 90^o nên OEIF là hình chữ nhật và OE = OF nên OEIF là hình vuông OE = OF = EI

Mà AB = IA + IB = 6cm EB = 3cm EI = EB – IB = 1cm nên OE = OF = 1cm

Vậy tổng khoảng cách từ tâm đến hai dây là AB, CD là 2cm

Đáp án cần chọn là: D

Câu 2:

Cho đường tròn (O; R) có hai dây AB, CD bằng nhau và vuông góc với nhau tại I. Giả sử IA = 6cm; IB = 3cm. Tổng khoảng cách từ tâm O đến dây AB, CD là:

A. 4cm

B. 1cm

C. 3cm

D. 2cm

Xem đáp án

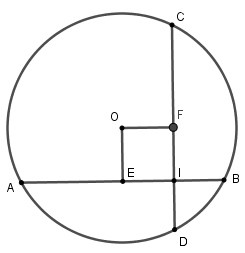
Xét đường tròn tâm (O)

Kẻ OEAB tại E suy ra E là trung điểm của AB, kẻ OFCD tại F.

Vì dây AB = AC nên OE = OF (hai dây bằng nhau cách đều tâm)

Xét tứ giác OEIF có = 90^o nên OEIF là hình chữ nhật và OE = OF nên OEIF là hình vuông OE = OF = EI

Mà AB = IA + IB = 9cm EB = 4,5cm EI = EB – IB = 1,5cm nên OE = OF = 1,5cm

Vậy tổng khoảng cách từ tâm đến hai dây là AB, CD là 1,5 + 1,5 = 3cm

Đáp án cần chọn là: C

Câu 3:

Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau ở M. Biết AB = 16cm; CD = 12cm; MC = 2cm. Khoảng cách từ tâm O đến dây AB là?

A. 4cm

B. 5cm

C. 3cm

D. 2cm

Xem đáp án

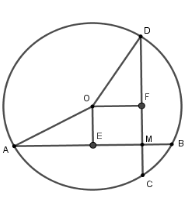
Xét đường tròn tâm (O)

Kẻ OEAB tại E suy ra E là trung điểm của AB, kẻ OFCD tại F suy ra F là trung điểm CD

Xét tứ giác OEMF có nên OEIF là hình chữ nhật, suy ra FM = OE

Ta có CD = 12cm FC = 6cm mà MC = 2cm FM = FC – MC = 4cm nên

OE = 4cm

Vậy khoảng cách từ tâm O đến dây AB là 4cm

Đáp án cần chọn là: A

Câu 4:

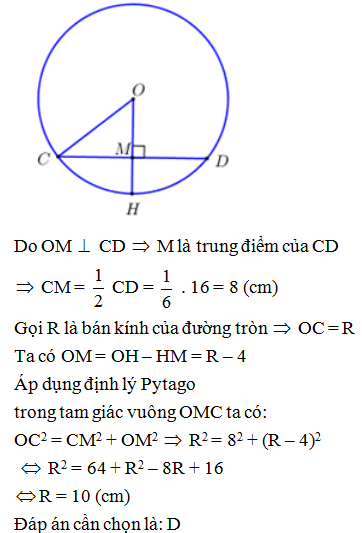
Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau ở M. Biết CD = 8cm; MC = 1cm. Khoảng cách từ tâm O đến dây AB là?

A. 4cm

B. 5cm

C. 3cm

D. 2cm

Xem đáp án

Kẻ OEAB tại E suy ra E là trung điểm của AB, kẻ OFCD tại F suy ra F là trung điểm CD

Xét tứ giác OEMF có nên OEIF là hình chữ nhật, suy ra FM = OE

Ta có CD = 8cm FC = 4cm mà MC = 1cm FM = FC –MC = 4 – 1 = 3cm

nên OE = FM = 3cm

Vậy khoảng cách từ tâm O đến dây AB là 3cm

Đáp án cần chọn là: C

Câu 5:

Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau ở M. Biết AB = 14cm; CD = 12cm; MC = 2cm. Bán kinh R và khoảng cách từ tâm O đến dây CD lần lượt là:

A. 8cm; $\sqrt{29}$ cm

B. $\sqrt{65}$ cm; $\sqrt{29}$ cm

C. $\sqrt{29}$ cm; $\sqrt{65}$ cm

D. $\sqrt{29}$ cm; 8cm

Xem đáp án

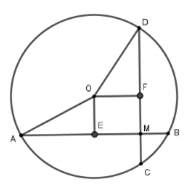
Lấy E, F lần lượt là trung điểm của hai dây AB và CD. Khi đó:

OEAB; OFAC lại có = 90^o nên OEMF là hình chữ nhật. Suy ra OE = MF = CF – MC = 4cm

Xét đường tròn tâm (O)

Có OE = 4cm, E là trung điểm của AB nên AE = $\frac{14}{2}$ =7cm

Áp dụng định lý Pytago cho tam giác vuông OEA ta có

OA = $\sqrt{A E^{2} + O E^{2}} = \sqrt{65}$ nên R = $\sqrt{65}$

Lại có OD = $\sqrt{65}$ cm; FD = 6cm nên áp dụng định lý Pytago cho tam giác vuông OFD ta có OF = $\sqrt{O D^{2} - F D^{2}} = \sqrt{29}$ .

Do đó khoảng cách từ tâm đến dây CD là $\sqrt{29}$ cm

Đáp án cần chọn là: B

Câu 6:

Cho đường tròn (O; R) có hai dây AB, CD vuông góc với nhau ở M. Biết AB = 10cm; CD = 8cm; MC = 1cm. Bán kinh R và khoảng cách từ tâm O đến dây CD lần lượt là:

A. $\sqrt{34}$ cm; 9cm

B. 6cm; 3cm

C. $\sqrt{34}$ cm; 3 $\sqrt{2}$ cm

D. $3 \sqrt{2}$ cm; $\sqrt{34}$ cm

Xem đáp án

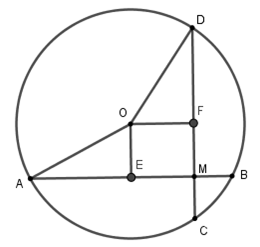
Xét đường tròn (O).

Kẻ OEAB tại E suy ra E là trung điểm của AB, kẻ OFCD tại F suy ra F là trung điểm của CD

Xét tứ giác OEMF có $\hat{E} = \hat{F} = \hat{M} = 90^{o}$ nên OEIF là hình chữ nhật, suy ra FM = OE

Ta có CD = 8cm FC = 4cm mà MC = 1cm FM = FC – MC = 4 – 1 = 3cm

nên OE = FM = 3cm

E là trung điểm của AB nên AE = $\frac{10}{2}$ = 5cm

Áp dụng định lý Pytago cho tam giác vuông OEA ta có:

OA = $\sqrt{A E^{2} + O E^{2}} = \sqrt{34}$ nên R = $\sqrt{34}$

Lại có OD = R = $\sqrt{34}$ ; FD = $\frac{C D}{2}$ = 4 nên áp dụng định lý Pytago cho tam giác vuông OFD ta có:

OF = $\sqrt{O D^{2} - F D^{2}} = \sqrt{34 - 16} = 3 \sqrt{2}$ . Do đó khoảng cách từ tâm đến dây CD là

3 $\sqrt{2}$ cm

Đáp án cần chọn là: C

Câu 7:

Cho nửa đường tròn (O), đường kính AB và một dây CD. Kẻ AE và BF vuông góc với CD lần lượt tại E và F. So sánh độ dài CE và DF

A. CE > DF

B. CE = 2DF

C. CE < DF

D. CE = DF

Xem đáp án

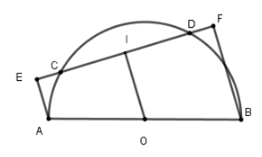
Lấy I là trung điểm EF

Xét tứ giác AEFB có AE // FB (vì cùng vuông với EF) nên AEFB là hình thang vuông tại E, F

Ta có OI là đường trung bình của hình thang AEFB nên OI // AE // FB OIEF

Hay OICD nên I là trung diểm CD (quan hệ giữa dây và đường kính)

Ta có IE = IF; IC = ID IE – IC = IF – ID EC = DF

Đáp án cần chọn là: D

Câu 8:

Cho nửa đường tròn (O), đường kính AB và một dây MN. Kẻ AE và BF vuông góc với MN lần lượt tại E và F. So sánh độ dài OE và OF.

A. OE = OF

B. OE = $\frac{3}{2}$ OF

C. OE < OF

D. OE > OF

Xem đáp án

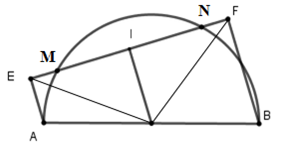
Lấy I là trung điểm EF

Xét tứ giác AEFB có AE // FB (vì cùng vuông với EF) nên AEFB là hình thang vuông tại E, F

Ta có OI là đường trung bình của hình thang AEFB nên OI // AE // FB OIEF

Hay OICD nên I là trung diểm CD (quan hệ giữa dây và đường kính)

Xét tam giác OEF có OI vừa là đường cao vừa là đường trung tuyến nên OEF cân tại O

Suy ra OE = OF

Đáp án cần chọn là: A

Câu 9:

Cho đường tròn (O), đường kính AB. Kẻ hai dây AC và BD song song. So sánh độ dài AC và BD

A. AC > BD

B. AC < BD

C. AC = BD

D. AC = 3BD

Xem đáp án

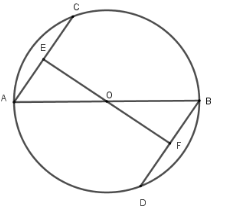
Kẻ đường thẳng qua O vuông góc với A tại E và cắt BD tại F thì EFBD tại F vì AC // BD.

Xét hai tam giác vuông OEA và tam giác OFB có OB = OA; $\hat{E A O} = \hat{F B O}$ (so le trong)

Nên (ch-gn) OE = OF AC = DB (hai dây cách đều tâm thì bằng nhau)

Đáp án cần chọn là: C

Câu 10:

Cho đường tròn (O), đường kính AB. Lấy điểm C là trung điểm đoạn OB. Kẻ dây MN qua C và dây AD//MN. So sánh độ dài AD và MN

A. AD = 2.MN

B. AD = MN

C. AD > MN

D. AD < MN

Xem đáp án

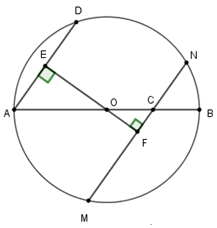
Kẻ đường thẳng qua O vuông góc với AD tại E và cắt MN tại F thì EF MN tại F vì AC // MN

Xét hai tam giác vuông OEA và tam giác OFC có $\hat{A E O} = \hat{O F C}$ = 90^o; $\hat{A O E} = \hat{F O C}$ (đối đỉnh)

Nên $Δ A E O$ $∽$ $Δ C F O$ (g – g) $\frac{O E}{O F} = \frac{O A}{O C}$ mà OA = OB = 2.OC

$\frac{O E}{O F} = \frac{O A}{O C}$ = 2 OE = 2OF

Hay OE > OF suy ra AD < MN (dây nào xa tâm hơn thì dây đó nhỏ hơn)

Đáp án cần chọn là: D

Câu 11:

Cho đường tròn (O; 10cm). Dây AB và CD song song, có độ dài lần lượt là 16cm và 12cm. Tính khoảng cách giữa 2 dây.

A. 14cm

B. 10cm

C. 12cm

D. 16cm

Xem đáp án

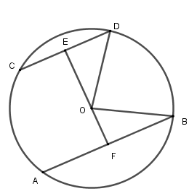
Kẻ đường thẳng qua O vuông góc với CD tại E và cắt Db tại F thì EF AB vì AB // CD

Khi đó E là trung điểm của CD và F là trung điểm của AB (đường kính vuông góc với dây thì đi qua trung điểm dây đó). Nên ED = 6cm; FB = 8cm; OD = OB= 10cm

Áp dụng định lý Pytago cho tam giác vuông OED ta được:

OE = $\sqrt{O D^{2} - E D^{2}}$ = 8cm

Áp dụng định lý Pytago cho tam giác vuông OFB ta được:

OF = $\sqrt{O B^{2} - F B^{2}}$ = 6cm

Vậy khoảng cách giữa hai dây là EF = OE + OF = 14cm

Đáp án cần chọn là: A

Câu 12:

Cho đường tròn (O; 8cm). Dây AB và CD song song, có độ dài lần lượt là 14cm và 10cm. Tính khoảng cách giữa 2 dây.

A. 2 $\sqrt{15}$ (cm)

B. 2 $\sqrt{39}$ (cm)

C. $\frac{\sqrt{38} + \sqrt{15}}{2}$ (cm)

D. $\sqrt{39} + \sqrt{15}$ (cm)

Xem đáp án

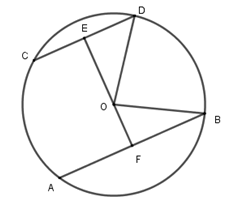
Kẻ đường thẳng qua vuông góc với CD tại E và cắt AB tại F thì EF AB vì AB // CD

Khi đó E là trung điểm của CD và F là trung điểm của AB (đường kính vuông góc với dây thì đi qua trung điểm dây đó).

Nên ED = = 5cm; FB = $\frac{A B}{2}$ = 7cm; OD = OB = 8cm

Áp dụng định lý Pytago cho tam giác vuông OED ta được:

OE = $\sqrt{O D^{2} - E D^{2}}$ = $\sqrt{8^{2} - 5^{2}}$ = $\sqrt{39}$ cm

Áp dụng định lý Pytago cho tam giác vuông OFB ta được:

OF = $\sqrt{O B^{2} - F B^{2}}$ = $\sqrt{8^{2} - 7^{2}}$ = $\sqrt{15}$ cm

Vậy khoảng cách giữa hai dây là EF = OE + OF = $\sqrt{39} + \sqrt{15}$ (cm)

Đáp án cần chọn là: D

Câu 13:

Cho đường tròn (O; R). Hai dây AB, CD song song với nhau sao cho tâm O nằm trong dải song song tạo bởi AB, CD. Biết khoảng cách giữa hai dây đó bằng 11cm và AB = 10 $\sqrt{3}$ cm, CD = 16cm. Tính R

A. R = 5 $\sqrt{2}$ (cm)

B. R = 10 $\sqrt{2}$ (cm)

C. R = 10 (cm)

D. R = 5 $\sqrt{3}$ (cm)

Xem đáp án

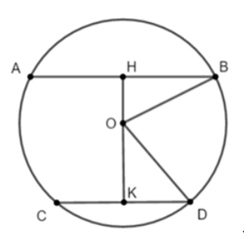
Kẻ OH AB; OK CD (H AB; K CD)

Theo bài ra ta có HK = 11 (cm)

Khi đó ta có H, K lần lượt là trung điểm của AB và CD (quan hệ vuông góc giữa đường kính và dây cung)

HB = $\frac{A B}{2}$ = 5 $\sqrt{3}$ (cm); KD = $\frac{C D}{2}$ = 8 (cm)

Áp dụng định lý Pytago ta có: OB² = OD² HB² + OH² = OK² + KD²

Đặt OH = x (0 < x < 11) OK = 11 – x

Khi đó ta có: HB² + x² = (11 – x)² + KD²

${(5 \sqrt{3})}^{2}$ + x² = (11 – x)² + KD² 75 + x² = x² – 22x + 121 + 64 x = 5 (tm)

Vậy R = OB = $\sqrt{{(5 \sqrt{3})}^{2} + 5^{2}}$ = 10 (cm)

Đáp án cần chọn là: C

Câu 14:

Cho tam giác ABC nhọn và có các đường cao BD, CE. So sánh BC và DE

A. BC = DE

B. BC < DE

C. BC > DE

D. BC = $\frac{2}{3}$ DE

Xem đáp án

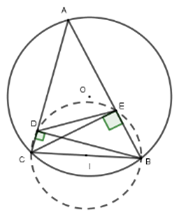
Lấy I là trung điểm của BC

Xét tam giác vuông BDC có DI là đường trung tuyến ứng với cạnh huyền nên

DI = IB = IC = $\frac{B C}{2}$

Xét tam giác vuông BEC có EI là đường trung tuyến ứng với cạnh huyền nên

EI = IB = IC = $\frac{B C}{2}$

Từ đó ID = IE = IB = IC = $\frac{B C}{2}$ hay bốn điểm B, C, D, E cùng thuộc đường tròn $(I; \frac{B C}{2})$

Xét $(I; \frac{B C}{2})$ có BC là đường kính và DE là dây không đi qua tâm nên BC > DE

Đáp án cần chọn là: C

Câu 15:

Cho hình vuông ABCD. Gọi M, N lần lượt là trung điểm của AB, BC. Gọi E là giao điểm của CM và DN. So sánh AE và DM

A. AM = $\frac{3}{2}$ AE

B. DM < AE

C. DM = AE

D. DM > AE

Xem đáp án

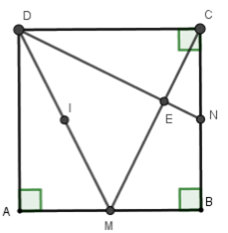
+ Ta có góc AND = góc ECN (vì cùng phụ với góc CNE) nên

$\hat{C N E} + \hat{E C N} = \hat{C N E} + \hat{C D N}$ = 90^o suy ra $\hat{C E N}$ = 90^oCMDN

+ Gọi I là trung điểm của DM

Xét tam giác vuông ADM ta có AI = ID = IM = $\frac{D M}{2}$ . Xét tam giác vuông DEM ta có EI = ID = IM = $\frac{D M}{2}$ nên EI = ID = IM = IA = $\frac{D M}{2}$

Do đó bốn điểm A, D, E, M cùng thuộc đường tròn tâm I bán kính R = $\frac{D M}{2}$

Xét $(I; \frac{D M}{2})$ có DM là đường kính và AE là dây không đi qua tâm nên DM > AE

Đáp án cần chọn là: D

Câu 16:

Cho đường tròn (O), đường kính AB = 14cm, dây CD có độ dài 12cm vuông góc với AB tại H nằm giữa O và B. Độ dài HA là?

A. 7 + $\sqrt{13}$ cm

B. 7 − $\sqrt{13}$ cm

C. 7cm

D. 7 − 2 $\sqrt{13}$ cm

Xem đáp án

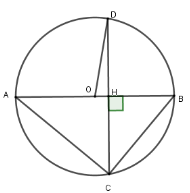
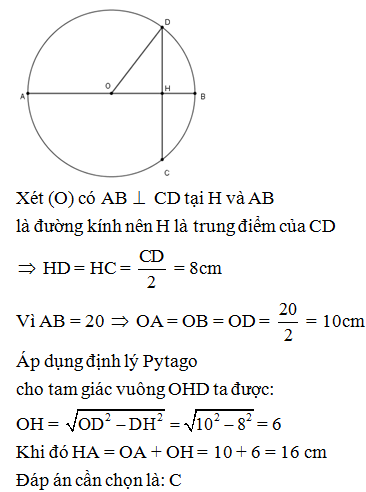
Xét (O) có AB CD tại H và AB là đường kính nên H là trung điểm của CD

HD = HC = $\frac{C D}{2}$ = 6cm

Vì AB = 14 OA = OB = OD = $\frac{14}{2}$ = 7cm

Áp dụng định lý Pytago cho tam giác vuông OHD ta được:

OH = $\sqrt{O D^{2} - D H^{2}} = \sqrt{13}$

Khi đó HA = OA + OH = 7 + $\sqrt{13}$ cm

Đáp án cần chọn là: A

Câu 17:

Cho đường tròn (O), đường kính AB = 20cm, dây CD có độ dài 16cm vuông góc với AB tại H nằm giữa O và B. Độ dài HA là?

A. 12cm

B. 18cm

C. 16cm

D. 15cm

Xem đáp án

Câu 18:

Cho đường tròn (O) và một dây CD. Từ O kẻ tia vuông góc với CD tại M, cắt (O; R) tại H. Biết CD = 16cm, MH = 4cm. Bán kính R bằng:

A. 12 $\sqrt{2}$ (cm)

B. 10 $\sqrt{2}$ (cm)

C. 12 (cm)

D. 10 (cm)

Xem đáp án

CHỌN BỘ SÁCH BẠN MUỐN XEM

Trắc nghiệm Đường kính và dây của đường tròn có đáp án

Trắc nghiệm Đường kính và dây của đường tròn có đáp án (Vận dụng)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương