Cho đường tròn (O; R) và điểm A nằm ngoài (O). Từ A, kẻ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC. Lấy D đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với (O) (E không trùng với D). Chọn câu đúng nhất:
A. Bốn điểm A, B, O, C cùng thuộc một đường tròn đường kính AC
B. BC là đường trung trực của OA
C. Cả A, B đều đúng
D. Cả A, B đều sai
Giải bởi Vietjack
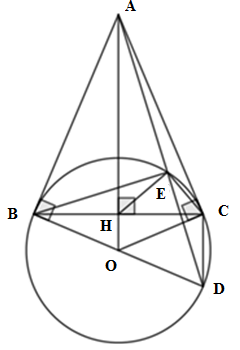
* Ta có AB, AC là hai tiếp tuyến của (O) OBA = OCA = 90o
B, C cùng thuộc đường tròn đường kính OA
A, B, O, C cùng thuộc một đường tròn đường kính OA. Do đó A sai.
* Ta có AB, AC là hai tiếp tuyến của (O) cắt nhau tại A
AB = AC và AO là phân giác BAC (tính chất 2 tiếp tuyến cắt nhau)
ABC là tam giác cân tại A
AO vừa là phân giác BAC vừa là đường trung trực của BC (tính chất tam giác cân) nên B sai
Đáp án cần chọn là: D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho đường tròn (O). Từ một điểm M ở ngoài (O), vẽ hai tiếp tuyến MA và MB sao cho góc AMB bằng 60o. Biết chu vi tam giác MAB là 24cm, tính độ dài bán kính đường tròn.
Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại I. Đường thẳng qua I và vuông góc với IA cắt OB tại K. Chọn khẳng định đúng.
Cho nửa đường tròn tâm O, đường kính AB. Vẽ các tiếp tuyến Ax, By với nửa đường tròn cùng phía đối với AB. Từ diểm M trên nửa đường tròn (M khác A, B) vẽ tiếp tuyến với nửa đường tròn, cắt Ax, By lần lượt tại C và D. Cho OD = BA = 2R. Tính AC và BD theo R
Cho đường tròn (O). Từ một điểm M ở ngoài (O), vẽ hai tiếp tuyến MA và MB sao cho góc AMB bằng 120o. Biết chu vi tam giác MAB là 6 (3 + 2)cm, tính độ dài dây AB
Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC, B (O) và C (O’). Tiếp tuyến chung trong tại A cắt tiếp tuyến chung ngoài BC tại I. Tính độ dài BC biết OA = 9cm, O’A = 4cm
Cho đường tròn (O; R) và điểm A nằm ngoài (O). Từ A, kẻ hai tiếp tuyến AB, AC với (O) (B, C là các tiếp điểm). Gọi H là giao điểm của OA và BC. Lấy D đối xứng với B qua O. Gọi E là giao điểm của đoạn thẳng AD với (O) (E không trùng với D). Tỉ số bằng?
Hai tiếp tuyến tại hai điểm B, C của một đường tròn (O) cắt nhau tại A tạo thành = 50o. Số đo của góc chắn cung nhỏ BC bằng:
Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Gọi D là trung điểm cạnh AC, tiếp tuyến của đường tròn (O) tại A cắt tia BD tại E. Chọn khẳng định đúng.
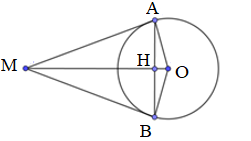
Cho hình vẽ, MA và MB là hai tiếp tuyến của đường tròn (O; 3cm), MA = 4cm. Độ dài đoạn thẳng AB là:
Cho tam giác ABC cân tại A, I là tâm đường tròn nội tiếp, K là tâm đường tròn bàng tiếp trong góc A. Gọi O là trung điểm của IK. Tâm của đường tròn đi qua bốn điểm B, I, C, K là:
Cho đường tròn (O), bán kính OA. Dây CD là đường trung trực của OA. Kẻ tiếp tuyến với đường tròn tại C, tiếp tuyến này cắt đường thẳng OA tại I. Biết OA = R. Tính CI theo R
Cho tam giác ABC cân tại A, I là tâm đường tròn nội tiếp, K là tâm đường tròn bàng tiếp trong góc A. Gọi O là trung điểm của IK. Tính bán kính đường tròn (O) biết AB = AC = 20cm, BC = 24cm
Cho tam giác ABC cân tại A nội tiếp đường tròn (O). Gọi D là trung điểm cạnh AC, tiếp tuyến của đường tròn (O) tại A cắt tia BD tại E. Tứ giác ABCE là hình gì?
Cho hai đường tròn (O); (O’) cắt nhau tại A, B, trong đó O’ (O). Kẻ đường kính O’OC của đường tròn (O). Chọn khẳng định sai?
1. Định lý về hai tiếp tuyến cắt nhau
Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì:
• Điểm đó cách đều hai tiếp điểm.
• Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
• Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
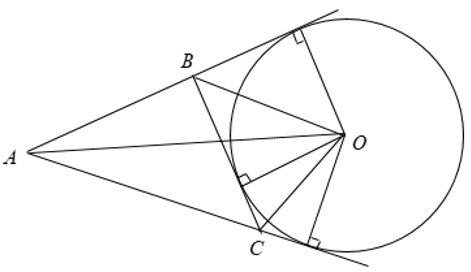
Ví dụ 1. Cho đường tròn (O) và điểm A nằm ngoài đường tròn. Từ điểm A kẻ hai tiếp tuyến AB và AC (B và C là tiếp điểm). Khi đó:
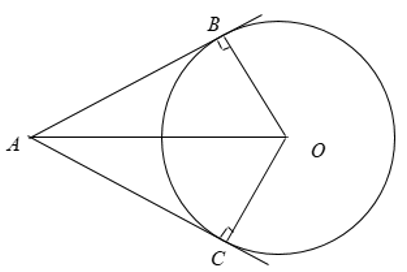
• Điểm A cách đều hai tiếp điểm B và C hay AB = AC.
• AO là tia phân giác của .
• OA là tia phân giác của .
2. Đường tròn nội tiếp của tam giác
Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với ba cạnh của tam giác, còn tam giác gọi là tam giác ngoại tiếp đường tròn.
Tâm của đường tròn nội tiếp tam giác là giao điểm của các đường phân giác các góc trong của tam giác.
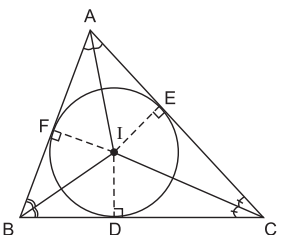
Ví dụ 2. Cho tam giác ABC. Gọi I là giao điểm của các đường phân giác các góc trong của tam giác; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ I đến các cạnh BC, AC, AB.
Khi đó, I là tâm đường tròn nội tiếp tam giác ABC hay tam giác ABC ngoại tiếp đường tròn tâm I.
3. Đường tròn bàng tiếp tam giác
Đường tròn bàng tiếp tam giác là đường tròn tiếp xúc với một cạnh của tam giác và tiếp xúc với các phần kéo dài của hai cạnh kia.
Tâm của đường tròn bàng tiếp trong góc A là giao điểm của hai đường phân giác các góc ngoài tại B và C, hoặc là giao điểm của đường phân giác góc A và đường phân giác góc ngoài tại B (hoặc C).
Với một tam giác, có ba đường tròn bàng tiếp.
Ví dụ 3. Cho tam giác ABC. Gọi K là giao điểm các đường phân giác của hai góc ngoài tại B và C; D, E, F theo thứ tự là chân các đường vuông góc kẻ từ K đến các đường thẳng BC, AC, AB.
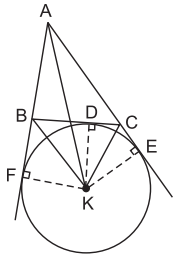
Khi đó, K là tâm đường tròn bàng tiếp tam giác ABC.
