Điền số thích hợp vào chỗ chấm
Tính giá trị biểu thức tại
Đáp số: A = …
 Giải bởi Vietjack
Giải bởi Vietjack
Bước 1: Đưa biểu thức về dạng (a + b)2
Bước 2: Áp dụng
Bước 3: Thay x vào biểu thức A
Lời giải
Thay vào biểu thức A đã rút gọn, ta có:
Vậy số cần điền vào chỗ chấm là −1
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Lựa chọn đáp án đúng nhất
Rút gọn biểu thức với y < 0 được kết quả là:
Điền số thích hợp vào chỗ chấm
Với và . Cho biểu thức
Với x = 4 thì M = …
Khẳng định sau Đúng hay Sai?
1. Căn bậc hai của 16 và 4
2. Với hai số a và b không âm, nếu a < b thì
3. xác định khi
Lựa chọn đáp án đúng nhất
Với . Kết quả phân tích thành nhân tử là:
Điền số thích hợp vào chỗ chấm
Giải phương trình
Tập nghiệm của phương trình là S = {…; …}
Điền đáp án vào chỗ chấm
Cho biểu thức (với x > 0 và )
Rút gọn P.
Đáp số: P = …
Điền số thích hợp vào chỗ chấm
Cho biểu thức (với x > 0 và )
Với P = 2 thì x = …
Điền số thích hợp vào chỗ chấm
Tính giá trị biểu thức:
Đáp án C = …
Điền số thích hợp vào chỗ chấm
Với và . Cho biểu thức
Tìm để
Đáp án: (các giá trị của x viết theo thứ tự tăng dần)
1. Căn bậc hai
a. Khái niệm: Căn bậc hai của một số a không âm là số x sao cho
b. Tính chất:
- Số âm không có căn bậc hai.
- Số 0 có đúng một căn bậc hai đó chính là số 0, ta viết .
- Số dương a có đúng hai căn bậc hai là hai số đối nhau; số dương ký hiệu là , số âm ký hiệu là .
2. Căn bậc hai số học
a. Định nghĩa: Với số dương a, số được gọi là căn bậc hai số học của a. Số 0 cũng được gọi là căn bậc hai số học của 0.
Chú ý. Với a ≥ 0, ta có:
Nếu thì x ≥ 0 và
Nếu x ≥ 0 và thì .
- Ta viết
b. Phép khai phương:
- Phép khai phương là phép toán tìm căn bậc hai số học của số không âm (gọi tắt là khai phương).
- Khi biết một căn bậc hai số học của một số, ta dễ dàng xác định được các căn bậc hai của nó.
3. So sánh các căn bậc hai số học
Định lí. Với hai số a và b không âm, ta có: .
4. Căn thức bậc hai
Với A là một biểu thức đại số, người ta gọi là căn thức bậc hai của A, còn A là biểu thức lấy căn hay còn gọi là biểu thức dưới dấu căn.
xác định (có nghĩa) khi A lấy giá trị không âm.
5. Hằng đẳng thức
Định lí. Với mọi số a, ta có .
Chú ý. Một cách tổng quát, với A là một biểu thức ta có , có nghĩa là:
nếu A ≥ 0 (tức là A lấy giá trị không âm);
nếu A < 0 (tức là A lấy giá trị âm).
6. Căn bậc hai của một tích
Định lí. Với hai số a và b không âm, ta có .
Chú ý: Định lí trên có thể mở rộng cho tích của nhiều số không âm.
7. Quy tắc khai phương một tích
Muốn khai phương một tích của các số không âm, ta có thể khai phương từng thừa số rồi nhân các kết quả lại với nhau.
(với a, b ≥ 0).
8. Quy tắc nhân các căn bậc hai
Muốn nhân các căn bậc hai của các số không âm, ta có thể nhân các số dưới căn với nhau rồi khai phương kết quả đó.
(với a, b ≥ 0).
Chú ý. Một cách tổng quát, với hai biểu thức A và B không âm ta có:
.
Đặc biệt, với biểu thức A không âm ta có:
.
9. Căn bậc hai của một thương
Định lí. Với số a không âm và số b dương, ta có: .
10. Quy tắc khai phương một thương
Muốn khai phương một thương , trong đó số a không âm và số b dương, ta có thể lần lượt khai phương của các số a và số b, rồi lấy kết quả thứ nhất chia cho kết quả thứ hai.
(với a ≥ 0, b > 0).
11. Quy tắc chia hai căn bậc hai
Muốn chia hai căn bậc hai của số a không âm và số b dương, ta có thể lấy số a chia cho số b rồi khai phương kết quả vừa tìm được.
(với a ≥ 0, b > 0).
Chú ý. Một cách tổng quát, với biểu thức A không âm và biểu thức B dương, ta có:
.
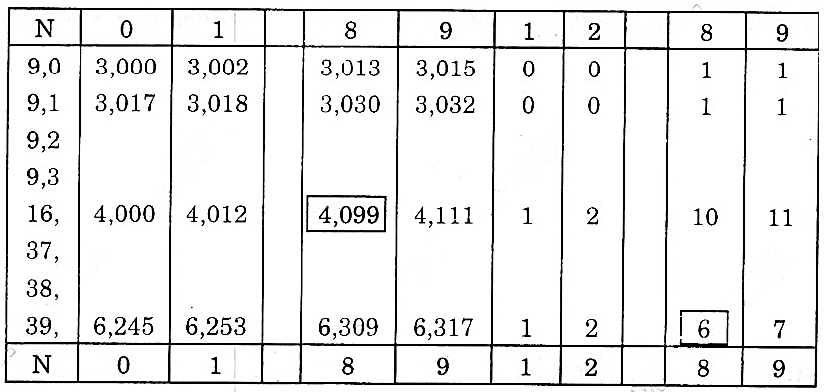
12. Giới thiệu bảng căn bậc hai
+ Bảng được chia thành các hàng và các cột.
+ Căn bậc hai của các số được viết bởi không qua ba chữ số từ 1,00 đến 99,9 được ghi sẵn trong bảng ở các cột từ cột 0 đến cột 9.
+ Tiếp đó là chín cột hiệu chính được dùng để hiệu chính chữ số cuối của căn bậc hai của các số được viết bởi bốn chữ số từ 1,000 đến 99,99.
+ Bảng căn bậc hai.
13. Đưa một thừa số ra ngoài dấu căn
• Với a ≥ 0, b ≥ 0, ta có: . Phép biến đổi này được gọi là phép đưa thừa số ra ngoài dấu căn.
• Đôi khi, ta phải biến đổi biểu thức dưới dấu căn về dạng thích hợp rồi mới thực hiện được phép đưa thừa số ra ngoài dấu căn.
• Có thể sử dụng phép đưa thừa số ra ngoài dấu căn để rút gọn biểu thức chứa căn thức bậc hai.
Tổng quát: Với hai biểu thức A, B mà B ≥ 0 ta có , tức là:
Nếu A ≥ 0 và B ≥ 0 thì ;
Nếu A < 0 và B ≥ 0 thì .
14. Đưa thừa số vào trong dấu căn
• Phép đưa thừa số ra ngoài dấu căn có phép biến đổi ngược với nó là phép đưa thừa số vào trong dấu căn.
Với A ≥ 0 và B ≥ 0 thì .
Với A < 0 và B ≥ 0 thì .
• Có thể sử dụng phép đưa thừa số vào trong (hoặc ra ngoài) dấu căn để so sánh các căn bậc hai.
15. Khử mẫu của biểu thức lấy căn
Tổng quát: Với các biểu thức A, B mà A. B ≥ 0 và B ≠ 0, ta có:
.
16. Trục căn thức ở mẫu
Trục căn thức ở mẫu số là biến đổi để biểu thức đó mất căn thức ở mẫu số.
Tổng quát:
• Với các biểu thức A, B mà B > 0 ta có:
.
• Với các biểu thức A, B, C mà ta có:
.
• Với các biểu thức A, B, C mà A ≥ 0, B ≥ 0, A ≠ B ta có:
.
17. Rút gọn biểu thức chứa căn thức bậc hai
- Để rút gọn biểu thức chứa căn bậc hai, ta cần vận dụng phối hợp các phép tính và các phép biến đổi đã biết.
- Khi rút gọn một dãy các phép tính cộng, trừ, nhân, chia, lũy thứa và khai phương thì thứ tự thực hiện: khai căn trước rồi đến lũy thừa, sau đó đến nhân, chia, cộng, trừ.
18. Khái niệm căn bậc ba
Định nghĩa: Căn bậc ba của một số thực a là số x sao cho
• Mỗi số a đều có duy nhất một căn bậc ba.
• Căn bậc ba của một số a được kí hiệu là (số 3 gọi là chỉ số căn).
• Phép lấy căn bậc ba của một số gọi là phép khai căn bậc ba.
Chú ý. Từ định nghĩa căn bậc ba, ta có .
Nhận xét:
- Căn bậc ba của số dương là số dương;
- Căn bậc ba của số âm là số âm;
- Căn bậc ba của số 0 là số 0.
19. Tính chất căn bậc ba
• a < b .
• .
• Với b ≠ 0, ta có: .