Từ điểm M nằm ngoài đường tròn (O) vẽ hai tiếp tuyến MA, MB với (O) tại A và B. Qua A vẽ đường thẳng song song với MB cắt đường tròn tại C

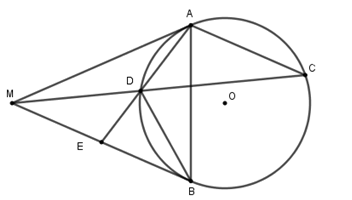
Nối C với M cắt đường tròn (O) tại D. Nối A với D cắt MB tại E. Chọn câu đúng

Cho hình vẽ, biết số đo cung BmD là 120^o. Khi đó:

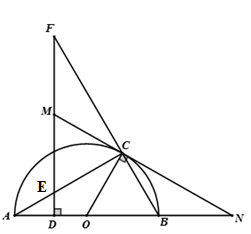
Cho điểm C thuộc nửa đường tròn (O) đường kính AB. Từ điểm D thuộc đoạn AO kẻ đường thẳng vuông góc với AO cắt AC và BC lần lượt tại E và F. Tiếp tuyến tại C với nửa đường tròn cắt EF tại M và cắt AB tại N. Khi đó:

Cho tam giác ABC cân tại A nội tiếp đường tròn tâm O. Trên (O) lấy điểm D thuộc cung AC. Gọi E = AC $\cap$ BD, F = AD $\cap$ BC. Khi đó mệnh đề đúng là:

Cho hai đường tròn (O; R) và (O’; R’) cắt nhau tại A và B. Vẽ cát tuyến CAD vuông góc với AB (C $\in$ (O), D $\in$ (O’)). Tia CB cắt (O’) tại E, tia DB cắt (O) tại F. Khi đó

Cho nửa đường tròn tâm O đường kính AB = 2R. Đường thẳng qua O và vuông góc AB cắt cung AB tại C. Gọi E là trung điểm BC. AE cắt nửa đường tròn O tại F. Đường thẳng qua C và vuông góc AF tại G cắt AB tại H. Khi đó góc $\widehat{OGH}$ có số đo là:

: Cho đường tròn (O; R) và dây cung BC = R. Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau tại A. Gọi M là giao điểm của AO và BC. Khi đó tam giác AMB là:

Qua điểm A nằm ngoài đường tròn (O) kẻ hai cát tuyến ABC và ADE với đường tròn đó (B nằm giữa A và C, D nằm giữa A và E). Kẻ dây BF // DE. Khi đó kết luận đúng là:

Cho đường tròn (O; R) và một điểm M bên trong đường tròn đó. Qua M kẻ hai dây cung AB và CD vuông góc với nhau (C thuộc cung nhỏ AB). Vẽ đường kính DE. Khi đó tứ giác ABEC là:

Cho tam giác nhọn ABC (AB > BC) nội tiếp đường tròn (O). D là điểm chính giữa cung AC. Giả sử {E} = AB $\cap$ CD, {F} = AD $\cap$  BC. Khi đó:

Cho tam giác nhọn ABC nội tiếp đường tròn (O), các đường cao AD, BE, CF (D $\in$ BC, E $\in$ AC, F $\in$ AB) cắt nhau tại H. Khi đó ta có:

Cho A là điểm cố định trên đường tròn (O; R). Gọi AB và AC là hai dây cung thay đổi trên đường tròn (O) thỏa mãn $\sqrt{AB.AC}$ = R$\sqrt{3}$. Khi đó vị trí của B, C trên (O) để diện tích ABC lớn nhất là:

Cho tam giác ABC nội tiếp đường tròn tâm O. Gọi P, Q, R lần lượt là giao điểm của các tia phân giác trong góc A, B, C với đường tròn. Giả sử rằng S = AP$\cap$  RQ. Khi đó

Tia phân giác góc $\widehat{BAD}$ của hình bình hành ABCD cắt các đường thẳng BC và DC lần lượt tại hai điểm M và N. Dựng ra phía ngoài hình bình hành ABCD tam giác MCO cân tại O với $\widehat{MOC}=\widehat{BAD}$ . Khi đó

Cho hình vuông ABCD có cạnh 2R.

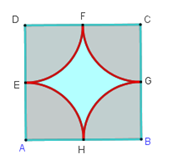
Diện tích S phần màu xanh trong hình vuông ABCD là: