Cho nửa đường tròn (O) đường kính AB và C là điểm chính giữa của cung AB. Lấy điểm M thuộc cung BC và điểm N thuộc tia AM sao cho AN = BM. Kẻ dây CD song song với AM. Gọi S₁; S₂ lần lượt là diện tích của tam giác CAN và tam giác BCM. (hình vẽ)

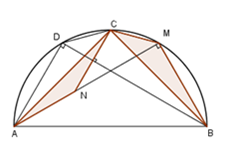
Khi đó tam giác AMN là tam giác:

Cho BC là một dây cung của đường tròn (O; R), (BC $\ne$ 2R). Điểm A di động trên cung lớn BC sao cho O luôn nằm trong tam giác ABC. Các đường cao AD, BE, CF của tam giác ABC đồng quy tại H. Chọn kết luận sai

Cho $∆$ABC nội tiếp đường tròn (O; R) có độ dài các cạnh là AB = c, BC = a; CA = b kẻ AH $\perp$ BC, AO cắt (O) tại D. Diện tích S của $∆$ABC là:

Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax, By. Trên Ax lấy điểm M rồi kẻ tiếp tuyến MP cắt By tại N. Khi đó tỉ số $\frac{S_{MON}}{S_{APB}}$ trong trường hợp AM = $\frac{R}{2}$  là:

Cho đường tròn (O; R), đường kính AB cố định, đường kính CD thay đổi (CD $\ne$ AB). Các tia BC, BD cắt tiếp tuyến của đường tròn (O) tại A lần lượt tại E, F. Khi CD thay đổi, giá trị nhỏ nhất của EF theo R là:

Cho tam giác ABC không cân, nội tiếp đường tròn (O), BD là đường phân giác của góc $\overbrace{\mathrm{ABC}}$ . Đường thẳng BD cắt đường tròn (O) tại điểm thứ hai là E. Đường tròn (O₁) đường kính DE cắt đường tròn (O) tại điểm thứ hai là F. Khi đó đường thẳng đối xứng với đường thẳng BF qua đường thẳng BD cắt AC tại N thì:

Cho nửa đường tròn (O) đường kính AB và C là điểm chính giữa của cung AB. Lấy điểm M thuộc cung BC và điểm N thuộc tia AM sao cho AN = BM. Kẻ dây CD song song với AM. Gọi S₁; S₂ lần lượt là diện tích của tam giác CAN và tam giác BCM. (hình vẽ)

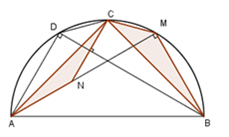
Chọn câu đúng.

Cho nửa đường tròn đường kính AB = 2R. Từ A và B kẻ hai tiếp tuyến Ax và By. Qua điểm M thuộc nửa đường tròn kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax, By lần lượt tại C và D. Khi đó độ dài AC + BD nhỏ nhất khi:

Cho hai đường tròn (O₁) và (O₂) có bán kính bằng R cắt nhau tại hai điểm A, B. Qua A vẽ cát tuyến cắt hai đường tròn (O₁) và (O₂) thứ tự tại E và F.  = 120^o. Khi đó diện tích S phần giao của hai đường tròn (O₁) và (O₂) là:

Cho đường tròn (O; R) và một điểm M nằm ở ngoài đường tròn sao cho MO = 2R. Đường thẳng d đi qua M, tiếp xúc với đường tròn (O; R) tại A. Giả sử N = MO $\cap$ (O; R). Kẻ hai đường kính AB, CD khác nhau của (O; R). Các đường thẳng BC, BD cắt đường thẳng d lần lượt tại P, Q. Khi đó:

Cho đường tròn (O; R) và một điểm M bên trong đường tròn đó. Qua M kẻ hai dây cung AB và CD vuông góc với nhau (C thuộc cung nhỏ AB). Vẽ đường kính DE. Cho biết thêm rằng R = 1. Giá trị lớn nhất của biểu thức Q = MA + MB + MC + MD là:

Cho BC là một dây cung của đường tròn (O; R), (BC $\ne$ 2R). Điểm A di động trên cung lớn BC sao cho O luôn nằm trong tam giác ABC. Các đường cao AD, BE, CF của tam giác ABC đồng quy tại H. Kẻ đường kính AK của đường tròn (O; R). Khi đó BHCK là:

Cho tam giác ABC cân tại A, nội tiếp đường tròn (O; R). Gọi D là trung điểm của AC; tia BD cắt tiếp tuyến tại A với đường tròn (O) tại điểm E; EC cắt (O) tại F. Giả sử rằng DF // BC. Khi đó cos $\widehat{ABC}$ = ?

Cho tam giác đều ABC có cạnh bằng 1, nội tiếp trong đường tròn tâm O. Đường cao AD của tam giác ABC cắt đường tròn tại điểm H. Diện tích phần giới hạn bởi cung nhỏ BC và hình BOCH là:

Cho đường tròn (O; R), đường kính AB cố định, đường kính CD thay đổi (CD $\ne$ AB). Các tia BC, BD cắt tiếp tuyến của đường tròn (O) tại A lần lượt tại E, F. Tứ giác ADCEF là:

Gọi M, N lần lượt là trung điểm của các cạnh AB, CD của hình chữ nhật ABCD. Biết rằng đường tròn ngoại tiếp hình chữ nhật ABCD có đường kính $d=\sqrt{8+2\sqrt{3}}$ và sự tồn tại điểm I thuộc đoạn MN sao cho $\widehat{DAI}$ = 45^o, $\widehat{IDA}$ = 30^o. Khi đó diện tích S của hình chữ nhật ABCD là: