Cho tứ giác ABCD có . Tổng số đo các góc ngoài đỉnh B, C, D bằng:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án cần chọn là: C

Gọi góc ngoài tại 4 đỉnh A, B, C, D của tứ giác ABCD lần lượt là .
Khi đó ta có :
Theo kết quả các câu trước ta có
Vậy
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Chọn câu đúng nhất trong các câu sau khi định nghĩa tứ giác ABCD:
Cho tứ giác ABCD có tổng số đo góc ngoài tại hai đỉnh B và C là . Tổng số đo các góc ngoài tại 2 đỉnh A, C là:
Cho tứ giác ABCD có . Tổng số đo các góc ngoài đỉnh B, C, D bằng:
Cho tứ giác ABCD. Tổng số đo các góc ngoài tại 4 đỉnh A, B, C, D là:
1. Định nghĩa tứ giác
Tứ giác ABCD là hình gồm bốn đoạn thẳng AB, BC, CD, DA trong đó bất kì đoạn thẳng nào cũng không cùng nằm trên một đường thẳng.
- Tứ giác ABCD còn được gọi tên là tứ giác BCDA, ADCB, ....
- Các điểm A, B, C, D được gọi là các đỉnh.
- Các đoạn thẳng AB, BC, CD, DA được gọi là các cạnh.
- Tứ giác ABCD trên hình gọi là tứ giác lồi.
• Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kì cạnh nào của tứ giác.
Chú ý. Khi nói đến tứ giác, ta hiểu đó là tứ giác lồi.
Ví dụ: Cho ABCD là tứ giác lồi.
Khi đó, tứ giác nằm trong nửa mặt phẳng có bờ là đường thẳng chứa AB, BC, CD hoặc DA của tứ giác ABCD.
2. Tổng các góc của một tứ giác
Định lí. Tổng các góc của một tứ giác bằng .
Ví dụ: Cho tứ giác ABCD trong đó có = 50o, = 140o, = 75o. Tính số đo của góc ?
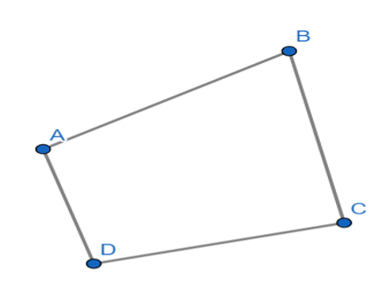
Hướng dẫn giải
Tứ giác ABCD ta có:
Vậy = .