Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN. Tứ giác BMNC là hình gì? Chọn đáp án đúng nhất.
A. Hình thang.
B. Hình thang cân.
C. Hình thang vuông.
D. Cả A, B, C đều sai.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án cần chọn là: B
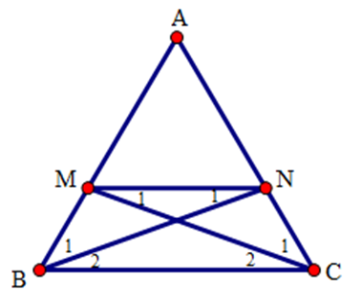
Ta có AB = AM + MB và AC = AN + NC
Mà AB = AC (do tam giác ABC cân tại A) và BM = NC (gt)
Suy ra AN = AM
Xét tam giác AMN cân tại A.
Suy ra .
Xét tam giác ANM có: (tổng ba góc trong một tam giác)
= (vì ) (1)
Xét tam giác ABC cân tại A ta có:
= (tổng ba góc trong một tam giác) nên = (vì ) (2)
Từ (1) và (2)
Mà , là hai góc đồng vị nên MN // BC
Xét tứ giác MNCB có MN // BC nên MNCB là hình thang.
Lại có (do ΔABC cân tại A) nên MNCB là hình thang cân.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Góc kề cạnh bên của hình thang có số đo là . Góc kề còn lại của cạnh bên đó là:
Góc kề cạnh bên của hình thang có số đo là . Góc kề còn lại của cạnh bên đó là:
Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho AD = AE. Tứ giác BDEC là hình gì?
Chọn đáp án đúng nhất.
Cho tam giác ΔAMN cân tại A. Các điểm B, C lần lượt trên các cạnh AM, AN sao cho AB = AC. Hãy chọn câu đúng:
Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho DE // BC.
Chọn đáp án đúng nhất. Tứ giác BDEC là hình gì? Chọn câu đúng nhất.
Cho hình thang cân ABCD có đáy nhỏ AB = 4cm, đường AH = 6cm, và . Độ dài đáy lớn CD bằng
Cho hình thang cân MNPQ (MN // PQ) có góc và hai đáy có độ dài 12cm, 40cm. Diện tích của hình thang cân là:
Cho hình thang cân MNPQ (MN // PQ) có góc và hai đáy có độ dài 8cm, 30cm. Diện tích của hình thang cân là:
Cho hình thang cân ABCD đáy nhỏ AB = 4cm, đáy lớn CD = 10cm, cạnh bên BC = 5cm thì đường cao AH bằng:
Cho hình thang cân ABCD đáy nhỏ AB = 12cm, đáy lớn CD = 22cm, cạnh bên BC = 13cm thì đường cao AH bằng:
Cho hình thang ABCD có , DC = BC = 2.AB, DC = 4cm. Tính góc ABC của hình thang.
1. Định nghĩa hình thang
Hình thang là tứ giác có hai cạnh đối song song.
Hai cạnh song song gọi là hai đáy.
Hai cạnh còn lại gọi là hai cạnh bên.
Ví dụ: Cho hình thang ABCD có AB và CD là hai cạnh đáy.
Khi đó, AB // CD; AD và BC là hai cạnh bên.
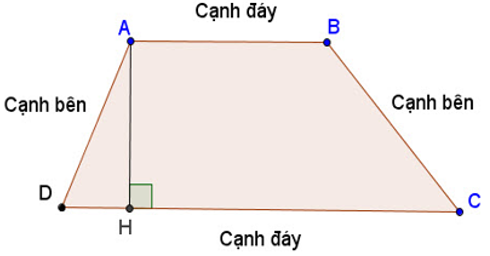
Gọi AH là đường vuông góc kẻ từ A đến đường thẳng CD.
Đoạn thẳng AH được gọi là đường cao của hình thang ABCD.
Nhận xét:
- Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau.
- Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau.
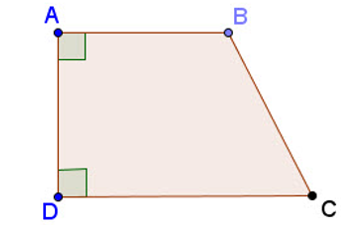
2. Hình thang vuông
Định nghĩa: Hình thang vuông là hình thang có một góc vuông.
Ví dụ: Cho hình thang ABCD có AB // CD, . Khi đó, (như hình vẽ).
Do đó, ABCD là hình thang vuông.