Trắc nghiệm Toán 8 Bài 2 Hình thang (có đáp án)
-
717 lượt thi
-
26 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Hãy chọn câu sai.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
+ Hình thang là tứ giác có hai cạnh đối song song nên A đúng.
+ Nếu một hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau, hai cạnh đáy bằng nhau nên B sai vì cạnh bên và cạnh đáy chưa chắc bằng nhau.
+ Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau nên C đúng.
+ Hình thang vuông là hình thang có một góc vuông nên D đúng.
Câu 2:
Câu nào sau đây là đúng khi nói về hình thang:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Theo định nghĩa: ”Hình thang là tứ giác có hai cạnh đối song song” nên A đúng.
Câu 3:
Chọn câu đúng nhất.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D.
+ Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
+ Trong hình thang cân, hai cạnh bên bằng nhau.
+ Trong hình thang cân, hai đường chéo bằng nhau.
Vậy cả A, B, C đều đúng
Câu 4:
Hình thang ABCD có . Số đo góc là:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
Vì tổng các góc của một tứ giác bằng nên
Câu 5:
Hình thang ABCD có . Số đo góc là:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Vì tổng các góc của một tứ giác bằng nên
Câu 6:
Góc kề cạnh bên của hình thang có số đo là . Góc kề còn lại của cạnh bên đó là:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
Vì tổng hai góc kề cạnh bên của hình thang bằng nên góc kề còn lại của cạnh bên đó có số đo bằng .
Câu 7:
Góc kề cạnh bên của hình thang có số đo là . Góc kề còn lại của cạnh bên đó là:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
Vì tổng hai góc kề cạnh bên của hình thang bằng nên góc kề còn lại của cạnh bên đó có số đo bằng .
Câu 8:
Cho tứ giác ABCD có BC = CD và DB là tia phân giác của góc D. Chọn khẳng định đúng
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
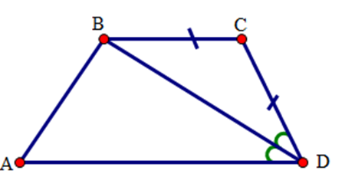
Xét ΔBCD có BC = CD (gt) nên ΔBCD là tam giác cân.
Suy ra
Vì DB là tia phân giác góc D của tứ giác ABCD nên
Do đó
Mà hai góc và là hai góc ở vị trí so le trong nên suy ra BC // AD.
Tứ giác ABCD có AD // BC (cmt) nên là hình thang.
Câu 9:
Cho tam giác ΔAMN cân tại A. Các điểm B, C lần lượt trên các cạnh AM, AN sao cho AB = AC. Hãy chọn câu đúng:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
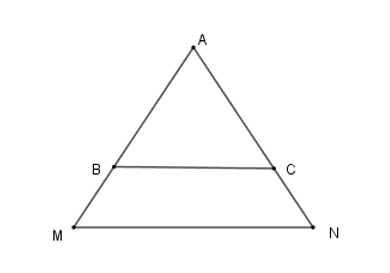
Xét ΔBAC có: BA = CA (gt) nên ΔBCA là tam giác cân.
Suy ra: (1) nên C đúng
Vì ΔAMN cân tại A => AM = AN mà AB = AC nên AM – AB = AN – AC ó MB = NC do đó A đúng.
Lại có: (2) (do ΔAMN cân tại A)
Từ (1) và (2) suy ra:
Mà hai góc và là hai góc ở vị trí đồng vị nên suy ra BC // MN
Tứ giác BCNM có: MN // BC (cmt) nên là hình thang.
Hình thang BCNM có: (cmt) nên là hình thang cân. Do đó, B đúng
Vậy cả A, B, C đúng
Câu 10:
Cho hình thang vuông ABCD có , AB = AD = 2cm, DC = 4cm. Tính góc ABC của hình thang.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D

Từ B kẻ BH vuông góc với CD.
Tứ giác ABHD là hình thang có hai cạnh bên AD // BH nên AD = BH, AB = DH.
Mặt khác, AB = AD = 2cm nên suy ra BH = DH = 2cm.
Do đó: HC = DC – HD = 4 – 2 = 2cm.
Tam giác BHC có BH = HC = 2cm nên tam giác BHC cân đỉnh H.
Lại có (do BH ⊥ CD) nên tam giác BHC vuông cân tại H.
Do đó
Xét hình thang ABCD có:
Vậy .
Câu 11:
Cho hình thang ABCD có , DC = BC = 2.AB, DC = 4cm. Tính góc ABC của hình thang.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
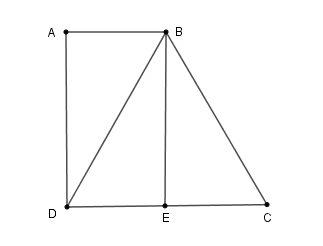
Từ B kẻ BE vuông góc với CD tại E.
Tứ giác ABED là hình thang có hai cạnh bên AD // BE nên AD = BE, AB = DE.
Mặt khác, DC = BC = 2AB nên DC = 2ED, do đó E là trung điểm của DC.
Xét ΔBDE và ΔBCE có ; DE = EC
BE cạnh chung nên ΔBED = ΔBEC (c – g – c)
Suy ra BD = BC mà BC = DC (gt) => BD = BC = CD nên ΔBCD đều.
Xét ΔBCD đều có BE là đường cao cũng là đường phân giác nên
Vì AD // BE mà nên (hai góc trong cũng phía bù nhau)
Từ đó
Vậy
Câu 12:
Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho AD = AE. Tứ giác BDEC là hình gì?
Chọn đáp án đúng nhất.
 Xem đáp án
Xem đáp án
Tam giác ADE có AD = AE (gt) nên tam giác ADE cân tại A.
Suy ra (1)
Tam giác ABC cân tại A (gt) nên (2)
Từ (1) và (2) suy ra
Mà 2 góc này là hai góc ở vị trí đồng vị nên suy ra DE // BC
Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang
Lại có (vì tam giác ABC cân tại A) nên BDEC là hình thang cân
Câu 13:
Cho tam giác ABC cân tại A. Gọi D, E theo thứ tự thuộc các cạnh bên AB, AC sao cho DE // BC.
Chọn đáp án đúng nhất. Tứ giác BDEC là hình gì? Chọn câu đúng nhất.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
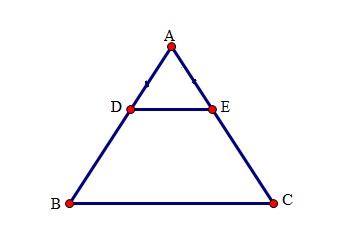
Tứ giác BDEC có DE // BC nên tứ giác BDEC là hình thang.
Lại có (vì tam giác ABC cân tại A) nên BDEC là hình thang cân
Câu 14:
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB, AC lần lượt tại D và E.
Chọn khẳng định đúng nhất?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: D
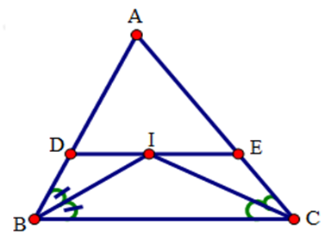
Xét tứ giác DECB có: DE // BC (gt) nên tứ giác DECB là hình thang.
Tương tự:
Tứ giác DICB có DI // BC (gt) nên tứ giác DICB là hình thang.
Tứ giác IECB có IE // CB (gt) nên tứ giác IECB là hình thang.
Câu 15:
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau tại I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB, AC lần lượt tại D và E.
Chọn khẳng định đúng.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
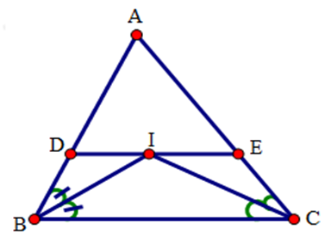
Vì DE // BC (gt) nên suy ra (so le trong)
Mà (gt) nên
Suy ra tam giác BDI cân đỉnh D.
Do đó DI = DB (1)
Ta có: IE // CB nên suy ra (so le trong)
Mà (gt) nên
Suy ra tam giác EIC cân đỉnh E
Do đó EI = EC (2)
Cộng (1) và (2) vế theo vế ta được: DI + EI = BD + CE
=> DE = BD + CE
Câu 16:
Cho hình thang cân MNPQ (MN // PQ) có góc và hai đáy có độ dài 12cm, 40cm. Diện tích của hình thang cân là:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
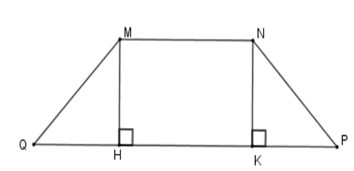
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK
Tứ giác MNKH có MN // HK nên MNKH là hình thang, lại có MH // NK
=> MN = HK; MH = NK
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có
MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNPK (ch – cgv)
=> QH = KP =
Mà HK = MN = 12 cm nên QH = KP = = 14 cm
Mà = => ΔMHQ vuông cân tại H => MH = QH = 14 cm
Diện tích hình thang cân MNPQ là
SMNPQ = = 364
Câu 17:
Cho hình thang cân MNPQ (MN // PQ) có góc và hai đáy có độ dài 8cm, 30cm. Diện tích của hình thang cân là:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
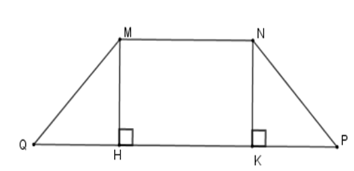
Kẻ MH ⊥ QP; NK ⊥ QP tại H, K => MH // NK
Tứ giác MNKH có MN // HK nên MNKH là hình thang, lại có MH // NK
=> MN = HK; MH = NK
(Vì hình thang có hai cạnh bên song song thì hai cạnh bên bằng nhau và hai cạnh đáy bằng nhau)
Lại có
MQ = NP (vì MNPQ là hình thang cân) suy ra ΔMQH = ΔNPK (ch – cgv)
=> QH = KP =
Mà HK = MN = 8 cm nên QH = KP = = 11 cm
Mà = => ΔMHQ vuông cân tại H => MH = QH = 11 cm
Diện tích hình thang cân MNPQ là
SMNPQ = = 209.
Câu 18:
Cho hình thang cân ABCD có đáy nhỏ AB = 4cm, đường AH = 6cm, và . Độ dài đáy lớn CD bằng
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
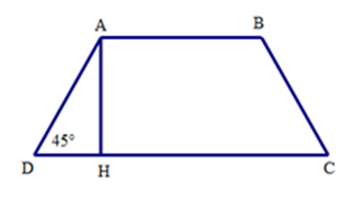
Ta có tam giác ADH vuông cân tại H vì = 450.
Do đó DH = AH = 6cm
Mà DH = (CD – AB)
Suy ra CD = 2DH + AB = 12 + 4 = 16 (cm)
Vậy CD = 16 cm.
Câu 19:
Cho hình thang cân ABCD có đáy nhỏ AB = 3cm, đường AH = 5cm, và . Độ dài đáy lớn CD bằng
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A.
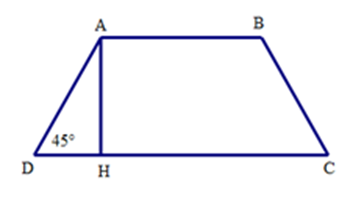
Ta có tam giác ADH vuông cân tại H vì = .
Do đó DH = AH = 5cm
Mà DH = (CD – AB)
Suy ra CD = 2DH + AB = 2.5 + 3 = 13 (cm)
Vậy CD = 13 cm
Câu 20:
Cho hình thang cân ABCD đáy nhỏ AB = 4cm, đáy lớn CD = 10cm, cạnh bên BC = 5cm thì đường cao AH bằng:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
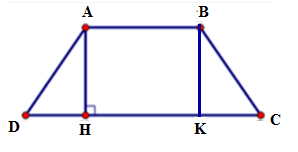
Kẻ BK ⊥ DC tại K.
Vì ABCD là hình thang cân nên ta có ; AD = BC
=> ΔAHD = ΔBKC (ch – gn) => DH = CK
Suy ra DH = (CD – AB)
Suy ra DH = (CD – AB) = (10 – 4) = 3 cm
Do ABCD là hình thang cân nên AD = BC = 5 cm
Áp dụng định lí Py-ta-go vào tam giác ADH vuông tại H ta có
Vậy AH = 4cm.
Câu 21:
Cho hình thang cân ABCD đáy nhỏ AB = 12cm, đáy lớn CD = 22cm, cạnh bên BC = 13cm thì đường cao AH bằng:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
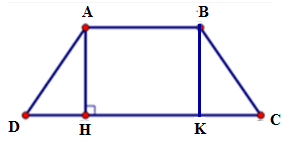
Ta có DH = (CD – AB) = (22 – 12) = 5 cm
Do ABCD là hình thang cân nên AD = BC = 13 cm
Áp dụng định lí Py-ta-go vào tam giác ADH vuông tại H ta có
Vậy AH = 12cm.
Câu 22:
Cho tam giác ABC cân tại A. Trên các cạnh bên AB, AC lấy các điểm M, N sao cho BM = CN. Tứ giác BMNC là hình gì? Chọn đáp án đúng nhất.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
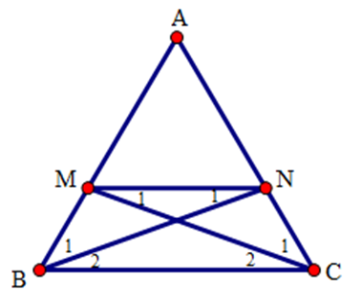
Ta có AB = AM + MB và AC = AN + NC
Mà AB = AC (do tam giác ABC cân tại A) và BM = NC (gt)
Suy ra AN = AM
Xét tam giác AMN cân tại A.
Suy ra .
Xét tam giác ANM có: (tổng ba góc trong một tam giác)
= (vì ) (1)
Xét tam giác ABC cân tại A ta có:
= (tổng ba góc trong một tam giác) nên = (vì ) (2)
Từ (1) và (2)
Mà , là hai góc đồng vị nên MN // BC
Xét tứ giác MNCB có MN // BC nên MNCB là hình thang.
Lại có (do ΔABC cân tại A) nên MNCB là hình thang cân.
Câu 23:
Cho hình thang cân ABCD (AB // CD) có hai đường chéo cắt nhau tại I, hai đường thẳng AD và BC cắt nhau ở K. Chọn khẳng định đúng:
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
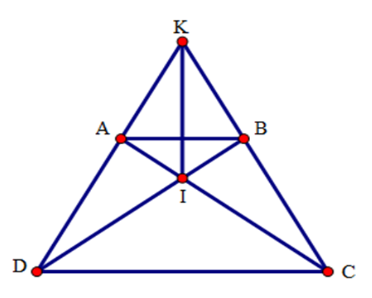
Xét tam giác ACD và tam giác BDC có:
+ AD = BC (do ABCD là hình thang cân)
+ AC = BD (do ABCD là hình thang cân)
+ CD là cạnh chung
Suy ra ΔACD = ΔBDC (c.c.c)
Suy ra , suy ra tam giác ICD cân tại I. Do đó ID = IC (1)
Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K.
Do đó KC = KD (2)
Từ (1) và (2) suy ra KI là đường trung trực của CD (*).
Xét tam giác ADB và tam giác BCA có:
+ AD = BC (cmt)
+ AB là cạnh chung
+ AC = BD
Suy ra ΔADB = ΔBCA (c.c.c)
Suy ra
Xét tam giác IAB có nên tam giác IAB cân tại I.
Do đó IA = IB (3)
Ta có KA = KD – AD; KB = KC – BC
Mà KD = KC, AD = BC, do đó KA = KB (4)
Từ (3) và (4) suy ra KI là đường trung trực của AB. (**)
Từ (*) và (**) suy ra KI là đường trung trực của hai đáy (đpcm)
Câu 24:
Cho hình thang cân ABCD (AB // CD) có hai đường chéo cắt nhau tại I, hai đường thẳng AD và BC cắt nhau ở K. Chọn câu sai.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: C
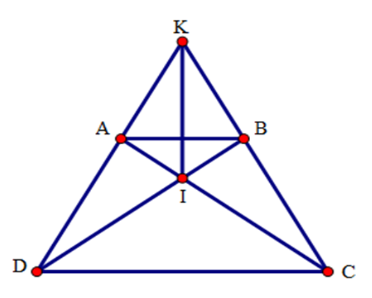
Xét tam giác ACD và tam giác BDC có:
+ AD = BC (do ABCD là hình thang cân)
+ AC = BD (do ABCD là hình thang cân)
+ CD là cạnh chung
Suy ra ΔACD = ΔBDC (c.c.c)
Suy ra (hai góc tương ứng), suy ra tam giác ICD cân tại I.
Nên C sai vì ta chưa đủ điều kiện để IC = CD
Tam giác KCD có hai góc ở đáy bằng nhau nên tam giác KCD cân ở K nên B đúng.
Xét tam giác KDI và tam giác KCI có:
+ KD = KC (do ΔKCD cân tại K))
+ KI là cạnh chung
+ IC = ID
Suy ra ΔKDI = ΔKCI (c.c.c)
Suy ra , do đó KI là phân giác nên D đúng.
Ta có AB // CD (do ABCD là hình thang) nên ; (các cặp góc đồng vị bằng nhau)
Mà (tính chất hình thang cân) nên (tính chất hình thang cân) nên ΔKAB cân tại K. Do đó A đúng
Câu 25:
Cho hình thang cân ABCD (AB // CD). Giả sử , chọn câu đúng.
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: A
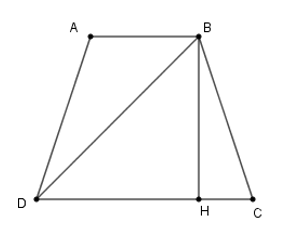
Kẻ BH ⊥ CD tại H.
Xét tam giác vuông BDH, theo định lý Pytago, ta có
Xét tam giác vuông CBH, theo định lý Pytago, ta có
Suy ra
(do DH + CH = CD, DH - CH = AB)
Câu 26:
Cho tam giác ABC vuông tại A, đường cao AH. Trên BC lấy điểm M sao cho CM = CA. Đường thẳng đi qua M và song song với CA cắt AB tại I.
Chọn câu đúng nhất. Tứ giác ACMI là hình gì?
 Xem đáp án
Xem đáp án
Đáp án cần chọn là: B
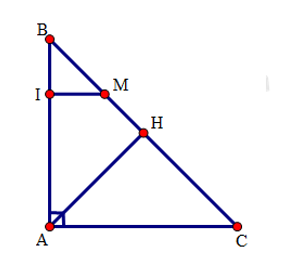
Tứ giác ACMI có: MI //AC (gt) và (gt) nên là hình thang vuông.
