Cho tam giác ABC có D, E lần lượt là trung điểm của AB, AC và DE = 4cm. Biết đường cao AH = 6cm. Diện tích của tam giác ABC là? 

1. Đường trung bình của tam giác

Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh của tam giác.

Ví dụ: Cho ∆ABC có D, E lần lượt là trung điểm của AB và AC (như hình vẽ).

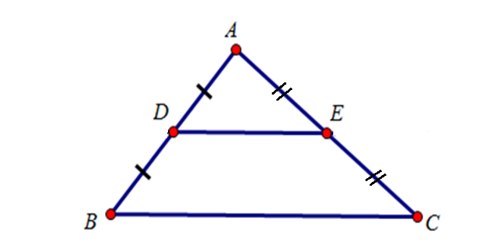
Khi đó, DE là đường trung bình của ∆ABC.

Định lí 1. Đường thẳng đi qua trung điểm một cạnh của tam giác và song song với cạnh thứ hai thì đi qua trung điểm cạnh thứ ba.

Ví dụ 1: Cho ΔABC có D là trung điểm của AB và DE // BC.

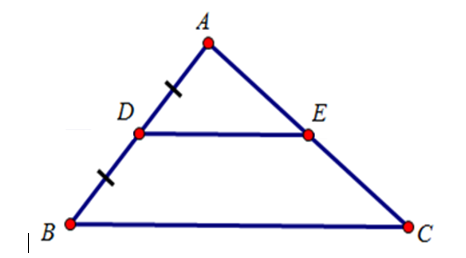
Khi đó, E là trung điểm của AC.

Định lí 2. Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.

Ví dụ 2: Cho ∆ABC có D, E lần lượt là trung điểm của AB và AC (như hình vẽ).

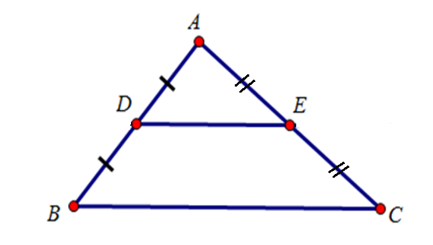
Khi đó, DE là đường trung bình của ∆ABC.

Do đó DE // BC và $DE=\frac{1}{2}BC$ .

2. Đường trung bình của hình thang

Định nghĩa: Đường trung bình của hình thang là đoạn thẳng nối trung điểm hai cạnh bên của hình thang.

Ví dụ 3: Cho hình thang ABCD có E, F lần lượt là trung điểm của AD và BC.

Khi đó, EF là đường trung bình của hình thang ABCD.

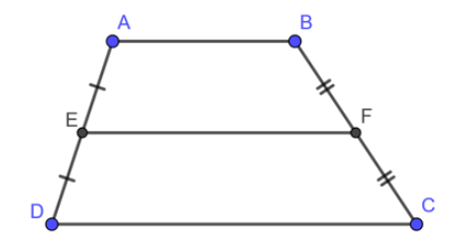
Định lí 3. Đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì đi qua trung điểm cạnh bên thứ hai.

Ví dụ 4: Cho hình thang ABCD có E lần lượt là trung điểm của AD và EF // CD.

Khi đó, F là trung điểm của hình thang BC.

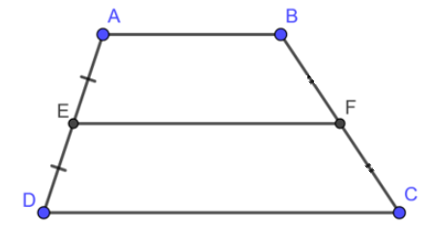
Định lí 4: Đường trung bình của hình thang thì song song với hai đáy và bằng nửa tổng hai đáy.

Ví dụ 5: Cho hình thang ABCD có EF là đường trung bình. Khi đó, EF // AB // CD,

$EF=\frac{AB+CD}{2}$.