Dựng hình thang cân ABCD, biết đáy CD = 3cm, đường chéo AC = 4cm, góc ∠D = 80o.
 Giải bởi Vietjack
Giải bởi Vietjack
a) Phân tích
Giả sử dựng được hình thang ABCD theo yêu cầu đề bài.
Ta dựng được đoạn thẳng CD = 3cm.
Điểm A phải thỏa mãn hai điều kiện:
+ Tia DA tạo với DC một góc bằng 80º.
+ CA = 4cm nên A thuộc cung tròn tâm C bán kính 4cm.
ABCD là hình thang nên AB // CD
Hình thang ABCD cân nên
Vì vậy điểm B phải thỏa mãn 2 điều kiện:
+ B nằm trên đường thẳng đi qua A và song song với CD
+ Tia CB tạo với CD một góc 80º.
b) Cách dựng
+ Dựng đoạn CD = 3cm.
+ Dựng tia Dx thỏa mãn
+ Dựng cung tròn tâm C, bán kính 4cm cắt tia Dx tại A.
+ Qua A dựng đường thẳng m song song với CD.
+ Dựng tia Cy trên cùng nửa mặt phẳng chứa điểm A, bờ CD thỏa mãn
+ Tia Cy cắt đường thẳng m tại B.
Ta dựng được hình thang ABCD
c) Chứng minh
+ Tứ giác ABCD là hình thang vì AB // CD
+ Hình thang ABCD có 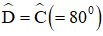
+ Hình thang cân ABCD có CD = 3cm, AC = 4cm, 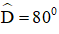
d) Biện luận: Ta luôn dựng được một hình thang thỏa mãn điều kiện đề bài.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Dựng tam giác ABC vuông tại A, biết cạnh huyền BC = 4cm, góc nhọn B = 65o.
Dựng tam giác ABC vuông tại B, biết cạnh huyền AC = 4cm, cạnh góc vuông BC = 2cm.
Dựng hình thang ABCD (AB // CD), biết AB = AD = 2cm, AC = DC = 4cm.
Dựng hình thang ABCD, biết ∠D = 90o, đáy CD = 3cm, cạnh bên AD = 2cm, cạnh bên BC = 3cm.
1. Bài toán dựng hình
Ta đã biết vẽ hình bằng nhiều dụng cụ: thước, compa, êke…. Ta xét các bài toán vẽ hình mà chỉ sử dụng hai dụng cụ là thước và compa, chúng được gọi là các bài toán dựng hình.
Với thước, ta có thể:
+ Vẽ được một đường thẳng khi biết hai điểm của nó.
+ Vẽ được một đoạn thẳng khi biết hai đầu mút của nó.
+ Vẽ được một tia khi biết gốc và một điểm của tia.
Với compa, ta có thể vẽ được một đường tròn khi biết tâm và bán kính của nó.
Ví dụ: Vẽ đường tròn tâm I có bán kính 3 cm.
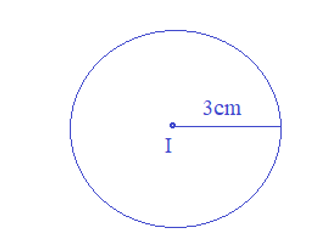
2. Các bài toán dựng hình đã biết
Chúng ta đã biết cách giải các bài toán dựng hình sau:
+ Dựng một đoạn thẳng bằng một đoạn thẳng cho trước.
Ví dụ: Dựng đoạn thẳng CD bằng đoạn thẳng AB cho trước.
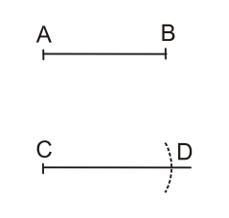
+ Dựng một góc bằng một góc cho trước.
Ví dụ: Dựng góc CID bằng số đo góc AOB cho trước.
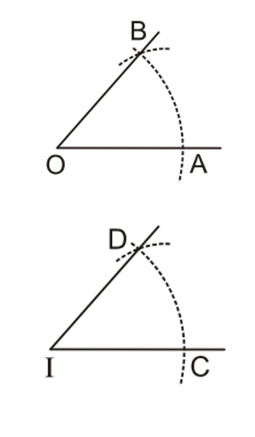
+ Dựng đường trung trực của một đoạn thẳng cho trước, dựng trung điểm của đoạn thẳng cho trước.
Ví dụ: Cho đoạn thẳng AB. Dựng đường thẳng CD là đường trung trực của đoạn thẳng AB.

+ Dựng tia phân giác của một góc cho trước.
Ví dụ: Dựng tia phân giác AC của góc AOB.
+ Qua một điểm cho trước, dựng đường thẳng vuông góc với một đường thẳng cho trước.
Ví dụ: Từ điểm A nằm ngoài đường thẳng BC. Dựng đường thẳng AD vuông góc với đường thẳng BC.

+ Qua một điểm nằm ngoài một đường thẳng cho trước, dựng đường thẳng song song với một đường thẳng cho trước.
Ví dụ: Từ điểm A nằm ngoài đường thẳng d, dựng đường thẳng qua A và song song với đường thẳng d.
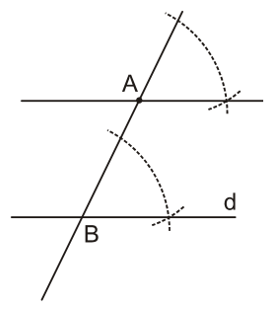
+ Các dạng dựng tam giác (biết ba cạnh, biết hai cạnh và góc xen giữa, một cạnh và hai góc kề).
3. Dựng hình thang
Ví dụ. Dựng hình thang ABCD biết đáy AB = 4 cm, đáy CD = 5 cm, cạnh bên AD = 3 cm, .
Hướng dẫn giải
a) Phân tích
Giả sử đã dựng được hình thang ABCD thỏa mãn yêu cầu của đề bài. Tam giác ACD dựng được vì biết hai cạnh và góc xen giữa. Điểm B phải thỏa mãn hai điều kiện:
+ B nằm trên đường thẳng đi qua A và song song với CD.
+ B cách A một khoảng 4 cm nên nằm trên đường tròn tâm A bán kính 4 cm.
b) Cách dựng
+ Dựng ∆ACD có , CD = 5 cm, AD = 3 cm.
+ Dựng tia Ax song song với DC (tia Ax và điểm C nằm trong cùng một nửa mặt phẳng bờ AD).
+ Dựng điểm B trên tia Ax sao cho AB = 4 cm. Kẻ đoạn thẳng BC.
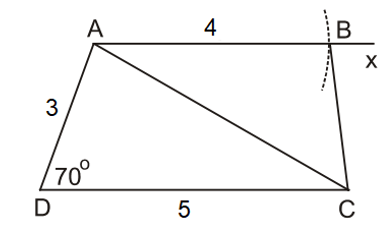
c) Chứng minh
Tứ giác ABCD là hình thang vì AB // CD.
Hình thang ABCD có AB = 4 cm, CD = 5 cm, AD = 3 cm, thỏa mãn yêu cầu bài toán.
d) Biện luận
Ta luôn dựng được một hình thang thỏa mãn điều kiện của đề bài.