Hãy chọn câu sai:
A. Điểm đối xứng với điểm M qua M cũng chính là điểm M
B. Hai điểm A và B gọi là đói xứng với nhau qua điểm O kkhi O là trung điểm của đoạn thẳng AB
C. Hình bình hành có một tâm đối xứng
D. Đoạn thẳng có hai tâm đối xứng
 Giải bởi Vietjack
Giải bởi Vietjack
+ Theo định nghĩa hai điểm đói xứng nhau qua một điểm: Hai điểm A, B gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó nên B đúng.
+ Trung điểm của đoạn thẳng là tâm đối xứng duy nhất của đoạn thẳng đó nên D sai.
+ Hình bình hành có một tâm đối xứng là giao hai đường chéo nên C đúng.
Điểm đối xứng của một điểm M qua chính M chính là M nên A đúng.
Đáp án cần chọn là: D
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Điền từ thích hợp vào chỗ trống. Hai điểm M, N gọi là đối xứng nhau qua điểm I nếu …
Cho hình bình hành ABEF. Gọi O là giao điểm của AE và BF. Trong các khẳng định sau:
Có bao nhiêu khẳng định đúng?
1. Hai điểm đối xứng qua một điểm
Định nghĩa: Hai điểm gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.
Ví dụ:

Hai điểm A và A’ gọi là hai điểm đối xứng với nhau qua điểm O.
Quy ước: Điểm đối xứng với điểm O qua điểm O cũng là điểm O.
2. Hai hình đối xứng qua một điểm
Định nghĩa: Hai hình gọi là đối xứng với nhau qua điểm O nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua điểm O và ngược lại.
Ví dụ:

Các điểm A’, B’, C’ lần lượt đối xứng với các điểm A, B, C qua O.
Khi đó, điểm O gọi là tâm đối xứng của tam giác ABC và tam giác A’B’C’.
3. Hình có tâm đối xứng
Định nghĩa: Điểm O gọi là tâm đối xứng qua hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua điểm O cũng thuộc hình H.
Ví dụ:
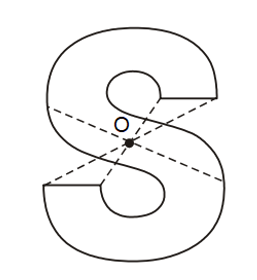
Chữ cái in hoa S có tâm đối xứng O (như hình vẽ).
Điểm đối xứng của mỗi điểm thuộc chữ in hoa S qua tâm đối xứng O đều thuộc chữ cái in hoa S.
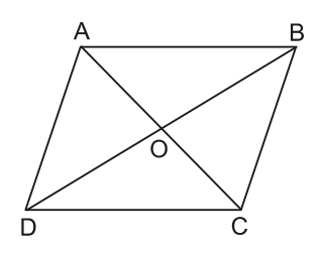
Định lí: Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.
Ví dụ: Hình bình hành ABCD, hai đường AC và BD cắt nhau tại điểm O.
Khi đó, O là tâm đối xứng của hình bình hành ABCD.