Hãy chọn câu sai:
A. Hình bình hành có tâm đối xứng là giao điểm của hai đường chéo
B. Đường tròn có tâm đối xứng chính là tâm của đường tròn
C. Hình thang có tâm đối xứng là giao điểm của hai đường chéo
D. Hình vuông có tâm đối xứng là giao điểm hai đường chéo
 Giải bởi Vietjack
Giải bởi Vietjack
+ Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó nên A đúng
+ Đường tròn là hình có hình có tâm đối xứng là tâm của đường tròn nên B đúng.
+ Giao điểm hai đường chéo của hình vuông là tâm đối xứng của hình vuông đó nên D đúng.
+ Hình thang không có tâm đối xứng nên C sai
Đáp án cần chọn là: C
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Điền từ thích hợp vào chỗ trống. Hai điểm M, N gọi là đối xứng nhau qua điểm I nếu …
Cho hình bình hành ABEF. Gọi O là giao điểm của AE và BF. Trong các khẳng định sau:
Có bao nhiêu khẳng định đúng?
1. Hai điểm đối xứng qua một điểm
Định nghĩa: Hai điểm gọi là đối xứng với nhau qua điểm O nếu O là trung điểm của đoạn thẳng nối hai điểm đó.
Ví dụ:

Hai điểm A và A’ gọi là hai điểm đối xứng với nhau qua điểm O.
Quy ước: Điểm đối xứng với điểm O qua điểm O cũng là điểm O.
2. Hai hình đối xứng qua một điểm
Định nghĩa: Hai hình gọi là đối xứng với nhau qua điểm O nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua điểm O và ngược lại.
Ví dụ:

Các điểm A’, B’, C’ lần lượt đối xứng với các điểm A, B, C qua O.
Khi đó, điểm O gọi là tâm đối xứng của tam giác ABC và tam giác A’B’C’.
3. Hình có tâm đối xứng
Định nghĩa: Điểm O gọi là tâm đối xứng qua hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua điểm O cũng thuộc hình H.
Ví dụ:
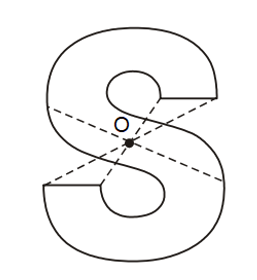
Chữ cái in hoa S có tâm đối xứng O (như hình vẽ).
Điểm đối xứng của mỗi điểm thuộc chữ in hoa S qua tâm đối xứng O đều thuộc chữ cái in hoa S.
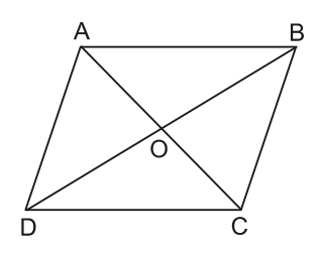
Định lí: Giao điểm hai đường chéo của hình bình hành là tâm đối xứng của hình bình hành đó.
Ví dụ: Hình bình hành ABCD, hai đường AC và BD cắt nhau tại điểm O.
Khi đó, O là tâm đối xứng của hình bình hành ABCD.