Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng 6cm, 8cm là:

1. Định nghĩa

Hình chữ nhật là tứ giác có bốn góc vuông.

Ví dụ: Tứ giác ABCD là hình chữ nhật $\iff$$\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}={90}^O$ .

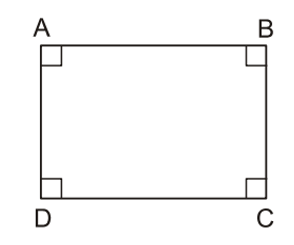
• Hình chữ nhật cũng là một hình bình hành và cũng là hình thang cân.

2. Tính chất

Hình chữ nhật là có tất cả các tính chất của hình bình hành và hình thang cân.

Ví dụ:

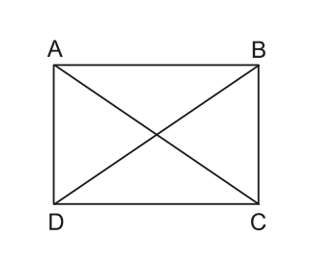
Hình chữ nhật ABCD có:

+ AB = CD và AD = BC (tính chất hình bình hành);

+ AC = BD (tính chất hình thang cân).

Định lí: Trong hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường.

Ví dụ: Hình chữ nhật ABCD có hai đường chéo AC và BD cắt nhau tại O.

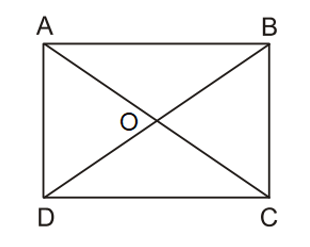
Khi đó, AC = BD và OA = OB = OC = OD.

3. Dấu hiệu nhận biết hình chữ nhật

• Tứ giác có ba góc vuông là hình chữ nhật.

• Hình thang cân có một góc vuông là hình chữ nhật.

• Hình bình hành có một góc vuông là hình chữ nhật.

• Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

Ví dụ: Cho tứ giác ABCD có ∆ABC vuông tại A, ∆BCD vuông tại B, ∆CDA vuông tại C. Tứ giác ABCD là hình gì?

Hướng dẫn giải

∆ABC vuông tại A nên $\widehat{BAC}$ = 90°

∆BCD vuông tại B nên $\widehat{CBD}$ = 90°

∆CDA vuông tại C nên $\widehat{DCA}$ = 90°

Mặt khác, tứ giác ABCD có:

$\widehat{BAC}$ + $\widehat{CBD}$ + $\widehat{DCA}$ + $\widehat{ADC}$ = 360°

 $\Rightarrow$$\widehat{ADC}$ = 360° − $\widehat{BAC}$ − $\widehat{CBD}$ − $\widehat{DCA}$

 $\Rightarrow \widehat{ADC}$  = 360° − 90° − 90° − 90° = 90°.

Vậy tứ giác ABCD là hình chữ nhật do có bốn góc vuông.

4. Áp dụng vào tam giác

• Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.

• Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.

Ví dụ: Cho tam giác ABC vuông tại A có AH là đường trung tuyến với cạnh huyền BC.

Khi đó,$HA=HB=HC=\frac{BC}{2}$ .