Cho hình thang ABCD (AB // CD) có diện tích , AB = 4cm, CD = 8cm. Gọi O là giao điểm của hai đường chéo. Tính diện tích tam giác COD
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Kẻ AH ⊥ DC; OK ⊥ DC tại H, K suy ra AH // OK
Chiều cao của hình thang:
Vì AB // CD (do ABCD là hình thang) nên theo định lý Ta-lét ta có
Vì AH // OK (cmt) nên theo định lý Ta-lét cho tam giác AHC ta có:
Do đó
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho tam giác ABC. Một đường thẳng song song với BC cắt các cạnh AB và AC theo thứ tự tại D và E. Qua E kẻ đường thẳng song song với CD, cắt AB ở F. Biết AB = 16, AF = 9, độ dài AD là:
Cho tam giác ABC có AB = 9cm, điểm D thuộc cạnh AB sao cho AD = 6cm. Kẻ DE song song với BC (E AC), kẻ EF song song với CD (F AB). Tính độ dài AF
Cho điểm M thuộc đoạn thẳng AB. Vẽ về một phía của AB các tam giác đều AMC và MBD. Gọi E là giao điểm của AD và MC, F là giao điểm của BC và DM.
1. Đặt MA = a, MB = b. Tính ME, MF theo a và b.
Cho hình thang ABCD (AB // CD) có diện tích , AB = 4cm, CD = 8cm. Gọi O là giao điểm của hai đường chéo. Tính diện tích tam giác COD
Cho điểm M thuộc đoạn thẳng AB. Vẽ về một phía của AB các tam giác đều AMC và MBD. Gọi E là giao điểm của AD và MC, F là giao điểm của BC và DM.
2. Tam giác MEF là tam giác gì? Chọn đáp án đúng nhất?
Cho điểm M thuộc đoạn thẳng AB sao cho MA = 2MB. Vẽ về một phía của AB các tam giác đều AMC và MBD. Gọi E là giao điểm của AD và MC, F là giao điểm của BC và DM.
2. Chọn khẳng định đúng nhất
Cho điểm M thuộc đoạn thẳng AB sao cho MA = 2MB. Vẽ về một phía của AB các tam giác đều AMC và MBD. Gọi E là giao điểm của AD và MC, F là giao điểm của BC và DM.
1. Đặt MB = a. Tính ME, MF theo a.
1. Định lý đảo
- Nếu một đường thẳng cắt hai cạnh một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
-
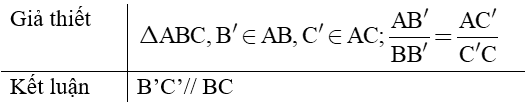
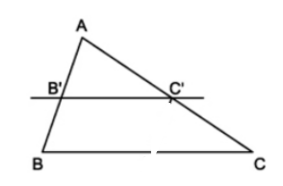
Ví dụ 1. Trong tam giác ABC có AB = 10cm; AC = 15cm. Lấy trên cạnh AB điểm B’, trên cạnh AC lấy điểm C’ sao cho AB’ = 4cm; AC’ = 6cm. Chứng minh B’C’// BC.
Lời giải:
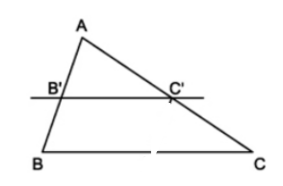
Ta có: B’B = AB – AB’ = 10 – 4 = 6cm,
Và CC’ = AC – AC’ = 15 – 6 = 9 cm
Ta có:
Theo định lí ta – lét đảo, suy ra: B’C’ // BC.
2. Hệ quả của định lý Ta – lét
- Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.
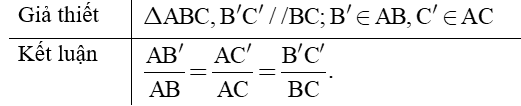
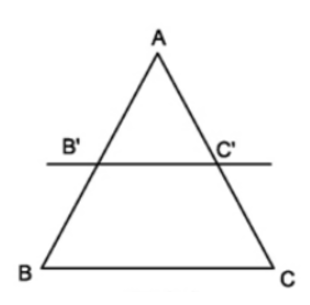
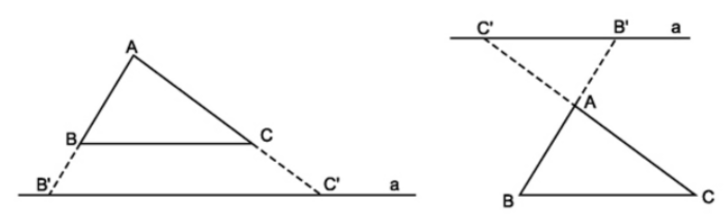
- Chú ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng song song với một cạnh và cắt phần kéo dài của hai cạnh còn lại.
Ví dụ 2. Trong tam giác ABC có AB = 6cm và B’C’// BC . Lấy trên cạnh AB điểm B’, trên cạnh AC lấy điểm C’ sao cho AB’ = 4cm; AC’ = 3cm. Tính độ dài cạnh AC.
Lời giải:
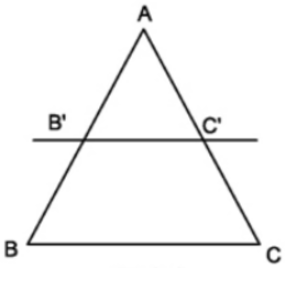
Áp dụng hệ quả trên ta có:
Khi đó ta có: