Cho ΔABC đồng dạng với ΔDEF và , AC = 6cm. Số đo góc là:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Xét tam giác ABC có:
Mà tam giác ABC đồng dạng với tam giác DEF nên
Vậy
Đáp án: B
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Hãy chọn câu đúng. Nếu tam giác ABC đồng dạng với tam giác MNP theo tỉ số k=2 thì tam giác MNP đồng dạng với tam giác ABC theo tỉ số:
Hãy chọn câu đúng. Tam giác ABC đồng dạng với tam giác MNP theo tỉ số , biết chu vi của tam giác ABC bằng 40 cm. Chu vi của tam giác MNP là:
Cho tam giác ABC đồng dạng với tam giác A’B’C’. Hãy chọn phát biểu sai:
Hãy chọn câu đúng. Cho tam giác ABC có AB = AC = 5cm, BC = 4 cm đồng dạng với tam giác MNP theo tỉ số . Chu vi của tam giác MNP là:
Hãy chọn câu đúng. Nếu tam giác ABC đồng dạng với tam giác MNP theo tỉ số k thì tam giác MNP đồng dạng với tam giác ABC theo tỉ số:
Hãy chọn câu trả lời đúng. Nếu tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số k thì tỉ số chu vi của tam giác A’B’C’ và ABC bằng
Cho tam giác ABC đồng dạng với tam giác A’B’C’. Hãy chọn phát biểu sai:
Cho tam giác ABC và hai điểm M, N lần lượt thuộc các cạnh BC, AC sao cho MN // AB. Chọn kết luận đúng.
Hãy chọn câu trả lời đúng. Nếu tam giác ABC đồng dạng với tam giác A’B’C’ theo tỉ số k thì tỉ số chu vi của hai tam giác đó bằng
Hãy chọn câu đúng. Hai ΔABC và ΔDEF có ; BC = 6cm. Nếu ΔABC đồng dạng với ΔDEF thì:
Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD và ΔBDC. Chọn câu đúng nhất.
Cho tứ giác ABCD có đường chéo BD chia tứ giác đó thành hai tam giác đồng dạng ΔABD ⁓ ΔBDC. Chọn câu sai.
1.Tam giác đồng dạng
a) Định nghĩa
Tam giác A’B’C’ gọi là đồng dạng với tam giác ABC nếu:
và
Tam giác A’B’C’ đồng dạng với tam giác ABC được kí hiệu là ∆A’B’C’ ∆ ABC.
Tỉ số các cạnh tương ứng được gọi là tỉ số đồng dạng
b) Tính chất
Các tính chất của hai tam giác đồng dạng:
Tính chất 1. Mỗi tam giác đồng dạng với chính nó.
Tính chất 2. Nếu ∆ABC ∆ A’B’C’ thì ∆A’B’C’ ∆ ABC.
Tính chất 3. Nếu ∆A’B’C’ ∆ A”B”C” và ∆A”B”C” ∆ ABC thì ∆A’B’C’ ∆ ABC.
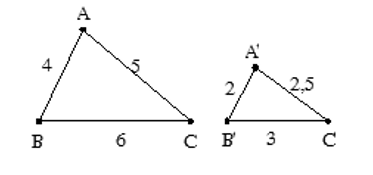
Ví dụ 1. Cho ∆A’B’C’ ∆ ABC như hình vẽ. Tính tỉ số đồng dạng ?
Lời giải:
Ta có ∆A’B’C’ ∆ ABC. Khi đó tỉ số đồng dạng là
2. Định lý
Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại tạo thành một tam giác đồng dạng với tam giác đã cho.
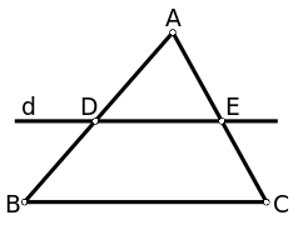

- Chú ý: Định lí cũng đúng cho trường hợp đường thẳng d cắt phần kéo dài của hai tam giác song song với cạnh còn lại.