Một tam giác có cạnh nhỏ nhất bằng 12, hai cạnh còn lại bằng x và y (x < y). Một tam giác khác có cạnh lớn nhất bằng 40,5, hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đó đồng dạng, từ đó suy ra giá trị của S = x + y bằng:
A. 45
B. 60
C. 55
D. 35
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Tam giác thứ nhất có các cạnh là 12 < x < y
Tam giác thứ hai có các cạnh là x < y < 40,5
Vì hai tam giác đồng dạng nên ta có x.y = 12.40,5 và .
Do đó nên suy ra x = 18
Suy ra
Vậy x = 18, y = 27 => S = 18 + 27 = 45
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Một tam giác có cạnh nhỏ nhất bằng 8, hai cạnh còn lại bằng x và y (x < y). Một tam giác khác có cạnh lớn nhất bằng 27, hai cạnh còn lại cũng bằng x và y. Tính x và y để hai tam giác đó đồng dạng.
Cho tam giác ABC. Các điểm D, E, F theo thứ tự làm trung điểm của BC, CA, AB. Các điểm A’, B’, C’ theo thứ tự là trung điểm của EF, DF, DE. Xét các khẳng định sau:
(I) ΔEDF ~ ΔABC theo tỉ số
(II) ΔA’B’C’ ~ ΔABC theo tỉ số
(III) ΔA’B’C’ ~ ΔEDF theo tỉ số k = 2
Số khẳng định đúng là:
Cho tam giác ABC. Các điểm D, E, F theo thứ tự làm trung điểm của BC, CA, AB. Các điểm A’, B’, C’ theo thứ tự là trung điểm của EF, DF, DE. Chọn câu đúng?
1. Định lí
- Nếu ba cạnh của tam giác này tỉ lệ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
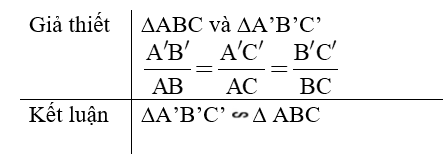
- Ví dụ 1. Cho ∆ABC và ∆A’B’C’ có độ dài các cạnh như hình vẽ.
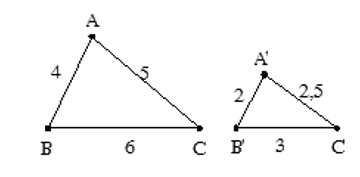
Ta có:
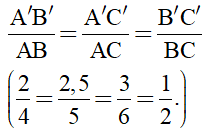
Do đó, ∆A’B’C’ ∆ ABC.