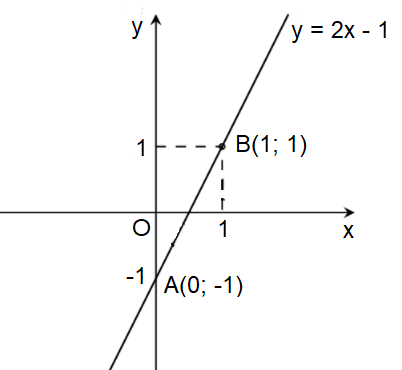Phương trình đường thẳng đi qua hai điểm A (1;4) và B (−1;0) có dạng
A. y = 2x + 2
B. y = −2x + 2
C. y = −2x + 4
D. y = 2x – 4
 Giải bởi Vietjack
Giải bởi Vietjack

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho hàm số bậc nhất y = (1 − 3m)x + m + 3.
Đồ thị của hàm số là đường thẳng đi qua gốc tọa độ khi m =
Cho hàm số y = f(x) = (m2 − 3m)x + m + 2. Tìm m để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng −2.
Cho hàm số bậc nhất y = (1 − 3m)x + m + 3. Tìm m để hàm số nghịch biến
Hãy chọn đáp án đúng
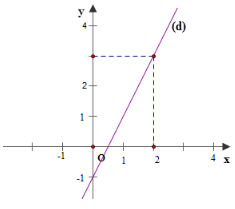
Đường thẳng (d) ở hình vẽ dưới là đồ thị của hàm số
Cho hàm số y = (m − 1) x + m có đồ thị là đường thẳng d. Tìm tọa độ điểm cố định I mà đồ thị hàm số luôn đi qua với mọi m. Tọa độ điểm I là (…; …)
Trên cùng một hệ trục tọa độ Oxy cho các đường thẳng:
y = x + 5 (d); y = −x + 1(d1)
Biết (d) Ox = A;(d1) Ox = B, (d) (d1) = M. Khi đó AMB là tam giác gì?
Vẽ đồ thị hàm số
Cho sẵn điểm O(0;0). (Hãy tìm thêm một điểm thuộc đồ thị để vẽ đồ thị hàm số )
Phương trình đường thẳng đi qua hai điểm A (0; −2) và B (−1; 3) có dạng
Trên cùng một hệ trục tọa độ Oxy cho các đường thẳng:
y = x + 5 (d); y = −x + 1(d1)
Biết (d) Ox = A;(d1) Ox = B, (d) (d1) = M.
Diện tích AMB là … (đơn vị diện tích)
Cho hàm số y = f(x) = (m2 − 3m)x + m + 2.
Tìm m để đồ thị hàm số đi qua điểm A(1;1).
Trên cùng một hệ trục tọa độ Oxy cho các đường thẳng:
y = x + 5 (d); y = −x + 1(d1)
Biết (d) (d1)=M. Tọa độ điểm M là
Cho hàm số y = (1 − 3m)x + m + 3 có đồ thị là đường thẳng (d). Tìm tọa độ điểm cố định I mà đồ thị hàm số luôn đi qua với mọi m. Tọa độ điểm I là
1. Đồ thị hàm số y = ax + b (a ≠ 0)
Đồ thị hàm số y = ax + b (a ≠ 0) là một đường thẳng:
- Cắt trục tung tại điểm có tung độ bằng b.
- Song song với đường thẳng y = ax nếu b ≠ 0; trùng với đường thẳng y = ax nếu b = 0
Chú ý. Đồ thị hàm số y = ax + b (a ≠ 0) còn được gọi là đường thẳng y = ax + b và b được gọi là tung độ gốc của đường thẳng.
Ví dụ 1. Gọi A là giao điểm của hai đường thẳng y = x − 1 và y = 3x + 1, tìm tọa độ của điểm A?
Lời giải:
Hoành độ giao điểm của hai đồ thị là nghiệm của phương trình:
x − 1 = 3x + 1
3x − x = − 1 − 1
2x = − 2
x = − 1.
Với x = − 1 thì y = − 1 − 1 = − 2. Khi đó, A(− 1; − 2).
Vậy tọa độ giao điểm A(− 1; − 2).
2. Cách vẽ đồ thị hàm số y = ax + b (a ≠ 0)
• Khi b = 0 thì y = ax. Đồ thị hàm số y = ax là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm A(1; a).
• Xét trường hợp y = ax + b với a ≠ 0 và b ≠ 0.
Bước 1: Cho x = 0 thì y = b, ta được điểm P(0; b) thuộc trục tung Oy.
Cho y = 0 thì , ta được điểm thuộc trục hoành Ox.
Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q ta được đồ thị hàm số y = ax + b (a ≠ 0).
Chú ý: Vì đồ thị y = ax + b (a ≠ 0) là một đường thẳng nên muốn vẽ nó chỉ cần xác định hai điểm phân biệt thuộc đồ thị.
Ví dụ 2. Vẽ đồ thị hàm số y = 2x – 1.
Bước 1: Cho x = 0 thì y = −1, ta được điểm A(0; −1) ∈ Oy.
Cho y = 1 thì 2x – 1 = 1 x = 1, ta được điểm B(1; 1)
Bước 2: Vẽ đường thẳng đi qua hai điểm A và B, ta được đồ thị hàm số y = 2x – 1.
Ta có đồ thị hàm số: