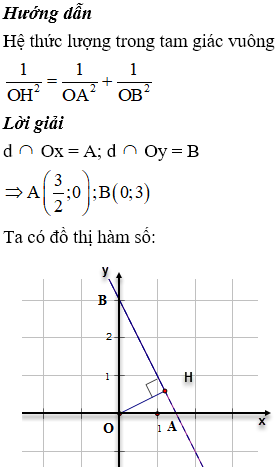
Cho đường thẳng d: y = −2x + 3; d  Ox = A; d  Oy = B

Khoảng cách từ điểm O đến đường thẳng d là

Hệ số góc của đường thẳng đi qua hai điểm A (1; 3) và B (2; 4) là:

Cho hàm số y = mx + 2m − 1. Tìm điểm cố định I mà đồ thị hàm số luôn đi qua với mọi m.
Tọa độ điểm I là 

Cho đường thẳng d: y = −x + 3. Khoảng cách từ gốc tọa độ O đến đường thẳng d là

Gọi $\alpha$ và $\beta$ lần lượt là góc tạo bởi đường thẳng y = 4x + 3 và y = 5x – 2 với trục Ox. Ta có:

Đường thẳng vuông góc với đường thẳng d: $y=-\frac{1}{3}x+5$ và đi qua điểm B (1; −4) có phương trình là:

Cho hàm số y = mx + 3m + 2. Tìm điểm cố định I mà đồ thị hàm số luôn đi qua với mọi m. Tọa độ điểm I là 

Điều kiện xác định của hàm số $y=\sqrt{16-x^2}+\frac{3}{x-3}$ là

Đường thẳng đi qua điểm A(1; 5) và cắt trục hoành tại điểm B có hoành độ bằng 2 có phương trình là

Đồ thị của hàm số y = |x| là

Cho hai hàm số bậc nhất  $y=\left(m-\frac{2}{3}\right)x+3$(1) và y = (2 – m)x + n – 1 (2)

Đồ thị của các hàm số (1) và (2) là hai đường thẳng song song với nhau khi

Cho đường thẳng d: y = 5x + 2. Tìm điểm M thuộc đường thẳng d sao cho điểm đó có hoành độ gấp bốn lần tung độ

Khẳng định sau Đúng hay Sai?

Hàm số y = f(x) = $\left(\sqrt{12-2\sqrt{35}}-\sqrt{7}\right)x+\sqrt{5}$ luôn đồng biến trên tập hợp số thực $\mathrm{ℝ}$

Cho hàm số y = (k² – 5k + 6)x – 5. Tìm k để hàm số nghịch biến

Đáp số: … < k < …

Cho đường thẳng d: y = −2x + 3; d$\cap$  Ox = A; d $\cap$ Oy = B

Khoảng cách từ điểm C (0; −2) đến đường thẳng d là 

Cho hàm số y = f(x) = (m² – 1)x² + (m – 5)x + 3. Tìm m để y = f(x) là hàm số bậc nhất nghịch biến