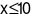 bằng cách liệt kê các phần tử.
bằng cách liệt kê các phần tử.
A.M = {1; 2; 3; 4; 5; 6; 7; 8; 9}
B. M = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10}
C. M = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}
D.M = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10}
 Giải bởi Vietjack
Giải bởi Vietjack
Ta có: 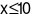 , nghĩa là x nhỏ hơn hoặc bằng 10.
, nghĩa là x nhỏ hơn hoặc bằng 10.
Các số tự nhiên x thỏa mãn x nhỏ hơn hoặc bằng 10 là: 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10. Vậy ta viết tập hợp M:
M = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10}.
Chọn đáp án D.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
I. Tập hợp các số tự nhiên
1. Tập hợp 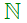 và tập hợp
và tập hợp 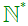
Các số 0, 1, 2, 3, 4 … là các số tự nhiên.
Tập hợp các số tự nhiên được kí hiệu là 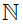 , tức là
, tức là 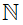 = {0; 1; 2; 3; 4; …} .
= {0; 1; 2; 3; 4; …} .
Tập hợp các số tự nhiên khác 0 được kí hiệu là  , tức là
, tức là 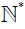 ={1; 2; 3; 4; …} .
={1; 2; 3; 4; …} .
2. Cách đọc và cách viết số tự nhiên
Ví dụ:
+ Số 12 134 355 đọc là mười hai triệu một trăm ba mươi tư nghìn ba trăm năm mươi lăm.
+ Số ba mươi ba nghìn bốn trăm năm mươi chín, viết là 33 459.
Chú ý: Khi viết các số tự nhiên có từ bốn chữ số trở lên, người ta thường viết tách riêng từng nhóm ba chữ số kể từ phải sang trái cho dễ đọc.
II. Biểu diễn số tự nhiên
1. Biểu diễn một số tự nhiên trên tia số
Các số tự nhiên được biểu diễn trên tia số. Mỗi số tự nhiên ứng với một điểm trên tia số.
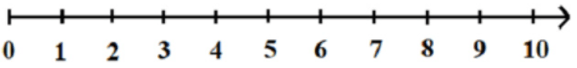
2. Cấu tạo thập phân của số tự nhiên
Số tự nhiên được viết trong hệ thập phân bởi một, hai hay nhiều chữ số. Các chữ số được dùng là 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Khi một số gồm hai chữ số trở lên thì chữ số đầu tiên (tính từ trái sang phải) khác 0.
Trong cách viết một số tự nhiên có nhiều chữ số, mỗi chữ số ở những vị trí khác nhau có giá trị khác nhau.
Ví dụ:
+ Số 987 có:
- Chữ số hàng trăm là 9 và có giá trị là 9 x 100
- Chữ số hàng chục là 8 và có giá trị là 8 x 10
- Chữ số hàng đơn vị là 7 và có giá trị là 7
Ta viết: 987 = 9 x 100 + 8 x 10 + 7
+ Kí hiệu 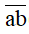 (a # 0) là chỉ số tự nhiên có hai chữ số có:
(a # 0) là chỉ số tự nhiên có hai chữ số có:
- Chữ số hàng chục là a và có giá trị là a x 10
- Chữ số hàng đơn vị là b và có giá trị là b
Ta viết: 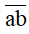 = a x 10 + b
= a x 10 + b
3. Số La Mã
Cách ghi số La Mã:
+ Các số tự nhiên từ 0 đến 10 được ghi bằng số La Mã tương ứng như sau:

+ Nếu thêm vào bên trái mỗi số ở dòng (1) một chữ số X, ta được số La Mã từ 11 đến 20:

+ Nếu thêm vào bên trái mỗi số ở dòng (1) hai chữ số X, ta được các số La Mã từ 21 đến 30:

Ví dụ:
+ Số La Mã XIV đọc là mười bốn
+ Số La Mã XXI đọc là hai mươi mốt
+ Số 15 được viết bằng số La Mã là: XV
+ Số 29 được viết bằng số La Mã là: XIX
III. So sánh các số tự nhiên
+ Trong hai số tự nhiên khác nhau, có một số nhỏ hơn số kia. Nếu số a nhỏ hơn số b thì ta viết a < b hay b > a.
Ví dụ: Số 15 nhỏ hơn số 20, ta viết 15 < 20 hay 20 > 15.
+ Với số tự nhiên a cho trước:
Ta viết x ≤ a để chỉ x < a hoặc x = a.
Ta viết x ≥ a để chỉ x > a hoặc x = a.
+ Nếu a < b và b < c thì a < c (tính chất bắc cầu)
Ví dụ: 2 < 3 và 3 < 4 thì 2 < 4
+ Cách so sánh hai số tự nhiên
- Trong hai số tự nhiên có số chữ số khác nhau: Số nào có nhiều chữ số hơn thì lớn hơn, số nào có ít chữ số hơn thì nhỏ hơn.
- Để so sánh hai số tự nhiên có số chữ số bằng nhau, ta lần lượt so sánh từng cặp chữ số trên cùng một hàng (tính từ trái sang phải) cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau. Ở cặp chữ số khác nhau đó, chữ số nào lớn hơn thì số tự nhiên chứa chữ số đó lớn hơn.
Ví dụ: So sánh: 1 000 999 và 998 999; 1 035 946 và 1 039 457
Lời giải:
+ Số 1 000 999 có bảy chữ số; số 998 999 có sáu chữ số.
Vậy 1 00 999 > 998 999.
+ Do hai số 1 035 946 và 1 039 457 có cùng số chữ số nên ta lần lượt so sánh từng cặp chữ số trên cùng một hàng kể từ trái sang phải cho đến khi xuất hiện cặp chữ số đầu tiên khác nhau là 5 < 9. Vậy 1 035 946 < 1 039 457.