Kết quả của phép tính 159 . 57 – 59 . 57 là:

I. Phép nhân 

1. Phép nhân hai số tự nhiên

a x b = c 

(thừa số) x (thừa số) = (tích)

Ví dụ: 5 x 2 = 10; 20 x 3 = 60 

Quy ước: 

+ Trong một tích, ta có thể thay dấu nhân “x” bằng dấu chấm “.” 

Ví dụ: 5 x 2 = 5 . 2 

+ Trong một tích mà các thừa số đều bằng chữ hoặc chỉ có một thừa số bằng số, ta có thể không cần viết dấu nhân giữa các thừa số

Ví dụ: a x b = a . b = ab hoặc 4. a . b = 4ab

+ Khi nhân hai số có nhiều chữ số, thông thường đặt tính rồi tính, chú ý khi viết các tích riêng (tích riêng thứ hai lùi sang bên trái một cột so với tích riêng thứ nhất, tích riêng thứ ba lùi sang bên trái hai cột so với tích riêng thứ nhất,…)
Ví dụ: Đặt tính rồi tính: 341 x 157

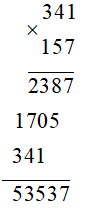
Vậy 341 x 157 = 53 537.

2. Tính chất của phép nhân

Phép nhân các số tự nhiên có các tính chất sau:

+ Giao hoán:               a . b = b . a

+ Kết hợp:                  (a . b) . c = a . (b . c)

+ Nhân với số 1:         a . a = 1 . a = a

+ Phân phối đối với phép cộng và phép trừ:

a . (b + c) = a. b + a . c

a . (b – c) = a . b – a . c

Chú ý: Do tính chất kết hợp nên giá trị của biểu thức a. b. c có thể được tính theo một trong hai cách sau:

a . b. c = (a . b) . c hoặc a . b . c = a . (b . c)

Ví dụ: Tính một cách hợp lý: 

a) 20 . 36 . 5 

b) 34 . 28 + 34 . 72 

Lời giải:

a) 20 . 36 . 5 

= 20 . 5 . 36           (tính chất giao hoán)

= (20 . 5) . 36         (tính chất kết hợp)

= 100 . 36 

= 3 600 

b) 34 . 28 + 34 . 72 

= 34 . (28 + 72) 

= 34 . 100 

= 3 400 

II. Phép chia

1. Phép chia hết 

a : b = q       (b#0) 

(số bị chia) : (số chia) = (thương)

Ví dụ: 10 : 2 = 5; 30 : 5 = 6

Chú ý: 

+ Nếu a : b = q thì q = bq

+ Nếu a : b = q và q  0 thì a : q = b 

+ Thông thường, ta đặt tính chia để thực hiện phép chia.

Ví dụ: Đặt tính để tính thương: 139 004 : 236.

Lời giải: 

Ta có: 

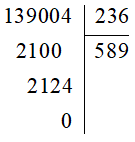
Vậy 139 004 : 236 = 589. 

2. Phép chia có dư

Cho hai số tự nhiên a và b với  . Khi đó luôn tìm được đúng hai số tự nhiên q và r sao cho a = b . q + r, trong đó  .

Chú ý: 

+ Khi r = 0 ta có phép chia hết.

+ Khi r # 0  ta có phép chia có dư. Ta nói: a chia cho b được thương là q và số dư là r.

Kí hiệu: a : b = q (dư r)

Ví dụ: Đặt tính để tính thương và số dư của phép chia: 

5 125 : 320.

Lời giải: 

Ta có: 

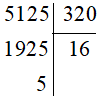
Vậy 5 125 : 320 = 16 (dư 5).