A.7
B.5
C.4
D.1
Giải bởi Vietjack
Ta có: 47 . 47 = 47 . (40 + 7) = 47 . 40 + 47 . 7
= 47 . 40 + (40 + 7) . 7
= 47 . 40 + 40 . 7 + 7 . 7
Suy ra 47 . 47 có chữ số tận cùng như chữ số tận cùng của 7 . 7 = 49.
Do đó 472có chữ số tận cùng là 9
Tương tự (472)2có chữ số tận cùng của 92= 81.
Mà (472)2= 472. 472= 47 . 47 . 47 . 47 = 474
Do đó 474có chữ số tận cùng là 1.
Vậy 475= 474. 47 có chữ số tận cùng là 1 . 7 = 7.
Chọn đáp án A.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
I. Phép nâng lên lũy thừa
Lũy thừa bậc n của a, kí hiệu , là tích của n thừa số a:
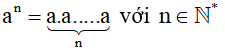
Trong đó:
a được gọi là cơ số
n được gọi là số mũ.
Quy ước: a1=a
Phép nhân nhiều thừa số bằng nhau gọi là phép nâng lên lũy thừa.
Chú ý:
+ an đọc là “a mũ n” hoặc “a lũy thừa n” hoặc “lũy thừa bậc n của a”.
+ a2 còn được gọi là “a bình phương” hay “bình phương của a”.
+ a3 còn được gọi là “a lập phương” hay “lập phương của a”.
Ví dụ:
7 . 7 . 7 . 7 = 74 (đọc là 7 mũ 4 hoặc là 7 lũy thừa 4, hoặc lũy thừa bậc bốn của 7)
16 = 2 . 2 . 2 . 2 = 24
Lưu ý: Với n là số tự nhiên khác 0, ta có: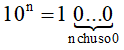 
Ví dụ: 105 = 10 . 10 . 10 . 10 . 10 = 100 000
II. Nhân hai lũy thừa cùng cơ số
Khi nhân hai lũy thừa cùng cơ số, ta giữ nguyên cơ số và cộng các số mũ:
am . an = am + n
Ví dụ:
+) 23 . 24 = 23 + 4 = 27
+) a2 . a1 = a2 + 1 = a3
+) 42 . 45 = 42 + 5 = 47
III. Chia hai lũy thừa cùng cơ số
Khi chia hai lũy thừa cùng cơ số (khác 0), ta giữ nguyên cơ số và trừ các số mũ:
am : an = am - n (a # 0, m ≥ n)
Quy ước: a0 = 1 (a # 0) .
Ví dụ:
+ 97 : 93 = 97 - 3 = 94
+ 76 : 7 = 76 : 71 = 76 - 1 = 75
+ 33 : 33 = 33 - 3 = 30 = 1
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số chẵn
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 2
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
