A. bằng b nếu a chia hết cho b
B.bằng a nếu a chia hết cho b
C.ước chung nhỏ nhất của a và b
D.hiệu của 2 số a và b
 Giải bởi Vietjack
Giải bởi Vietjack
Nếu a chia hết cho b thì b là ước của a.
Mà b cũng là ước của b nên là ước chung của a và b.
Hơn nữa b là ước lớn nhất của b nên ƯCLN (a, b) = b.
Vậy ƯCLN của a và b là bằng b nếu a chia hết cho b.
Chọn đáp án A.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Nếu 19 là số lớn nhất sao cho a ⁝ 19 và b ⁝ 19 thì 19 là ………. của a và b.
Nếu a ⁝ 7 và b ⁝ 7 thì 7 là ………. của a và b.
1. Chọn ra các thừa số nguyên tố chung
2. Phân tích mỗi số ra thừa số nguyên tố
3. Lấy tích các lũy thừa đã chọn, ta nhận được ước chung lớn nhất cần tìm
4. Với mỗi thừa số nguyên tố chung, ta chọn lũy thừa với số mũ nhỏ nhất
I. Ước chung và ước chung lớn nhất
1. Ước chung: Số tự nhiên n được gọi là ước chung của hai số a và b nếu n vừa là ước của a vừa là ước của b.
Quy ước: Viết tắt ước chung là ƯC.
Kí hiệu: Tập hợp các ước chung của a và b là ƯC(a, b).
Ví dụ: Ta có:
Các ước của 8 là: 1, 2, 4, 8
Các ước của 12 là: 1, 2, 3, 4, 6, 12
Do đó các ước chung của 8 và 12 là: 1, 2, 4.
Vậy ƯC(8, 12) = {1; 2; 4} .
Chú ý: Số tự nhiên n được gọi là ước chung của ba số a, b, c nếu n là ước của cả ba số a, b, c.
Ví dụ: Số 14 chia hết cho 7 nên 7 là ước của 14, 21 chia hết cho 7 nên 7 là ước của 21, 49 chia hết cho 7 nên 7 là ước của 49. Vậy 7 là ước chung của ba số 14, 21, 49.
2. Ước chung lớn nhất: Số lớn nhất trong các ước chung của hai số a và b được gọi là ước chung lớn nhất của a và b.
Quy ước: Viết tắt ước chung lớn nhất là ƯCLN.
Kí hiệu: ước chung lớn nhất của a và b là ƯCLN(a, b).
Ví dụ: Trong các ước chung của 8 và 12 là 1, 2, 4 thì 4 là số lớn nhất nên 4 là ước chung lớn nhất của 8 và 12. Ta viết ƯCLN(8, 12) = 4.
3. Tìm ước chung của hai số khi biết ƯCLN của hai số đó
Ước chung của hai số là ước của ước chung lớn nhất của chúng.
Ví dụ: Biết ƯCLN (a, b) = 60. Tìm tất cả các số có hai chữ số là ước chung của a và b.
Lời giải:
Vì ước chung của a và b đều là ước của ƯCLN (a, b) = 60 nên tất cả các số có hai chữ số là ước chung của a và b là: 10, 12, 15, 20, 30, 60.
II. Tìm ước chung lớn nhất bằng cách phân tích các số ra thừa số nguyên tố
Các bước tìm ƯCLN bằng cách phân tích ra thừa số nguyên tố:
Bước 1. Phân tích mỗi số ra thừa số nguyên tố
Bước 2. Chọn ra các thừa số nguyên tố chung
Bước 3. Với mỗi thừa số nguyên tố chung, ta chọn lũy thừa với số mũ nhỏ nhất
Bước 4. Lấy tích của các lũy thừa đã chọn, ta nhận được ước chung lớn nhất cần tìm.
Ví dụ: Tìm ƯCLN(54, 90).
+ Phân tích các số ra thừa số nguyên tố
54 = 2.33
90 = 2.32.5
Thừa số nguyên tố chung là 2 và 3. Số mũ nhỏ nhất của 2 là 1, số mũ nhỏ nhất của 3 là 2.
Vậy ƯCLN (54, 90) = 2.32 = 18.
Chú ý:
+ Nếu hai số đã cho không có thừa số nguyên tố chung thì ƯCLN của chúng bằng 1.
+ Nếu 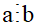 thì ƯCLN(a, b) = b. Chẳng hạn, ƯCLN(48, 16) = 16.
thì ƯCLN(a, b) = b. Chẳng hạn, ƯCLN(48, 16) = 16.
III. Hai số nguyên tố cùng nhau
1. Hai số nguyên tố cùng nhau
Hai số nguyên tố cùng nhau là hai số có ước chung lớn nhất bằng 1.
Ví dụ: Hai số 14 và 33 là hai số nguyên tố cùng nhau vì ƯCLN(14, 33) = 1.
2. Phân số tối giản
+ Phân số tối giản là phân số có tử và mẫu là hai số nguyên tố cùng nhau.
Ví dụ: Ta có: ƯCLN(4, 9) = 1 nên phân số 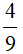 là phân số tối giản.
là phân số tối giản.
+ Ta có thể rút gọn một phân số về phân số tối giản bằng cách chia cả tử và mẫu của phân số đó cho ƯCLN của chúng.
Ví dụ: Rút gọn phân số 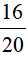 về phân số tối giản.
về phân số tối giản.
Ta có: ƯCLN(16, 20) = 4. Vậy 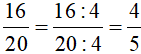 .
.