Cặp số (3; −11) là nghiệm của phương trình
A. 9,6x + y = 10,8
B. 3,2x – y = 20,6
C. 6,9x + 11y = 10,3
D. 3,2x – 2,3y = 17,5
 Giải bởi Vietjack
Giải bởi Vietjack

Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Trong mặt phẳng tọa độ Oxy, tập nghiệm của phương trình được biểu thị bởi đường thẳng
Hai phương trình 5x + 3y = 7 và 2x + 2y = 3 có cùng tập nghiệm đúng hay sai
Trong mặt phẳng tọa độ Oxy, tập nghiệm của phương trình 2x – y – 1 = 0(*) được biểu diễn bởi đường thẳng đi qua hai điểm M và N có tọa độ
Tìm m để đường thẳng x + y = m và đường thẳng 3x + 2y = 1 cắt nhau trên trục hoành
Tìm b để đường thẳng 2x – y = 5 và đường thẳng x + 3y = b cắt nhau tại một điểm trên trục tung
Nối mỗi cặp số ở cột A và một phương trình ở cột B sao cho cặp số này là nghiệm của phương trình đó
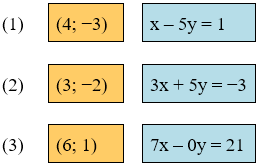
Tìm m để hai đường thẳng mx + 3y = 10 và phương trình x – 2y = 4 cắt nhau tại một điểm trên trục hoành
Đường thẳng d biểu diễn tập nghiệm của phương trình −0,01x – 0,01y = 0,02 là:
1. Khái niệm về phương trình bậc nhất hai ẩn
- Khái niệm phương trình bậc nhất hai ẩn: Phương trình bậc nhất hai ẩn x và y là hệ thức dạng ax + by = c (1)
trong đó a, b, c là các số đã biết ( hoặc )
Ví dụ 1:
2x + 3y = 5
4x + 6y = 7
-2x – 3y = 4
Các phương trình trên là những ví dụ về phương trình bậc nhất hai ẩn. Hai ẩn ở đây là x và y.
- Trong phương trình (1), nếu giá trị của vế trái tại x = x0 và y = y0 bằng vế phải thì cặp số (x0; y0) được gọi là một nghiệm của phương trình.
Ta cũng viết: Phương trình (1) có nghiệm là (x; y) = (x0; y0).
Chú ý:
- Trong mặt phẳng tọa độ Oxy mỗi nghiệm của phương trình ax + by = c được biểu diễn bởi một điểm. Nghiệm (x0; y0) được biểu diễn bởi điểm có tọa độ (x0; y0).
- Khái niệm tập nghiệm và khái niệm phương trình tương đương của phương trình bậc nhất hai ẩn cũng tương tự như đối với phương trình bậc nhất một ẩn. Ngoài ra ta cũng có thể áp dụng quy tắc chuyển vế hoặc quy tắc nhân đã học để biến đổi phương trình bậc nhất hai ẩn.
2. Tập nghiệm của phương trình bậc nhất hai ẩn
- Phương trình bậc nhất hai ẩn: ax + by = c luôn luôn có vô số nghiệm. Tập nghiệm của nó được biêu diễn bởi đường thẳng ax + by = c, kí hiệu là (d).
- Nếu và thì đường thẳng (d) chính là đồ thị của hàm số bậc nhất
- Nếu và b = 0 thì phương trình trở thành ax = c hay , và đường thẳng (d) song song với trục tung hoặc trùng với trục tung.
- Nếu a = 0 và thì phương trình trở thành by = c hay , và đường thẳng (d) song song hoặc trùng với trục hoành.
Nói cách khác, ta có công thức nghiệm tổng quát như sau:
- Nếu và thì công thức nghiệm là:
hoặc
Khi đó (d) cắt cả hai trục Ox; Oy
Ví dụ 2: x – y = 1 có và , khi đó công thức nghiệm là:
hoặc
- Nếu a = 0 và thì công thức nghiệm là:
và (d) // Ox
Ví dụ 3: Phương trình 0x + y = 5 có a = 0 và , khi đó công thức nghiệm là:
.
- Nếu và b = 0 thì công thức nghiệm là:
và (d) // Oy
Ví dụ 4: Phương trình 2x + 0y = 3 có và b = 0 , khi đó công thức nghiệm là:
.