(3 điểm):
Cho tam giác ABC, các điểm M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC. Trên tia đối của tia NP lấy điểm D sao cho ND = NP.a) Chứng minh: Tứ giác ADCP là hình bình hành.
b) Gọi F là giao điểm của MN và DC. Giả sử MN = 3cm. Tính BC và chứng minh FD = FC.
c) Gọi H là giao điểm của AP và MN; I là giao điểm của NP và HC. Chứng minh: B, I, F thẳng hàng.
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
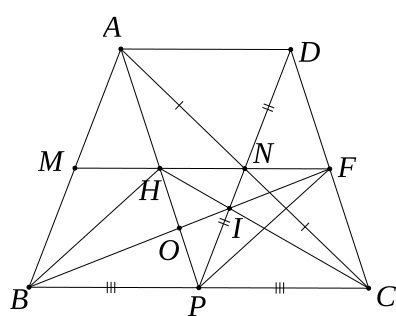
a) Xét tứ giác ADCP có:
N là trung điểm của AC
N là trung điểm của DP (ND = NP)
⇒ tứ giác ADCP là hình bình hành.
b) Xét tam giác ABC có:
M là trung điểm AB
N là trung điểm AC
⇒ MN là đường trung bình tam giác ABC
⇒ MN//BC, \(MN = \frac{1}{2}BC\)
⇒ BC = 2MN = 2.3 = 6cm
Ta có MN//BC (MN là đường trung bình tam giác ABC)
⇒ NF//PC
Trong tam giác DCP có:
N là trung điểm của DP
NF//PC
⇒ F là trung điểm của DC
Hay DF = FC
Suy ra NF là đường trung bình của ΔDCP.
\( \Rightarrow NF = \frac{1}{2}PC\)
c) Chứng minh tương tự: HN là đường trung bình của ΔACP và H là trung điểm của AP
\( \Rightarrow HN = \frac{1}{2}PC\)
Ta có: \(HF = HN + NF = \frac{1}{2}PC + \frac{1}{2}PC = PC\)
Mà có: PC = PB nên HN= PB
Xét tứ giác BHFP có HN = PB và HN // PB (vì MN//BC)
⇒ BHFP là hình hình hành
Gọi BF cắt HP tại O. Khi đó O là trung điểm của BF và HP.
Trong tam giác APC có CH và PN là đường trung tuyến
và CH cắt PN tại I
I là trọng tâm tam giác APC
\( \Rightarrow PI = \frac{2}{3}PN\)
Trong tam giác PHF có: PN là đường trung tuyến và \(PI = \frac{2}{3}PN\)
I là trọng tâm tam giác PHF
mà có FO là đường trung tuyến (vì O là trung điểm của HP)
I thuộc FO
F, I, O thẳng hàng
mà F, O, B thẳng hàng
nên B, I, F thẳng hàng.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
(0,5 điểm):
Tìm giá trị nhỏ nhất của biểu thức A, biết:A = x2+ 5y2– 4xy – 2y + 2x + 2010.
(2 điểm):
Phân tích các đa thức sau thành nhân tử:a) 6x2y – 4x3y;
b) 3(x + y) – x(x + y);
c) x2– 4xy + 4y2– z2;
d) 6x2(x – y) – (1 – x)(y – x).
a) y(12y + 3) + 4(7 – 3y2);
b) (x – 2)2– (3x + 1)(x – 3).
(1,5 điểm):
Tìm x biết:a) 15x2– 3x = 0;
b) (3x – 2)(x + 3) + (x2– 9) = 0;
c) (x – 1)3– (x + 1)(2 – 3x) = – 3.