a) Chứng minh tứ giác AECF là hình bình hành.
b) Gọi I là điểm đối xứng của A qua BD. Chúng minh EO là đường trung bình của tam giác AIC.
c) Chứng minh tứ giác CIDB là hình thang cân.
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
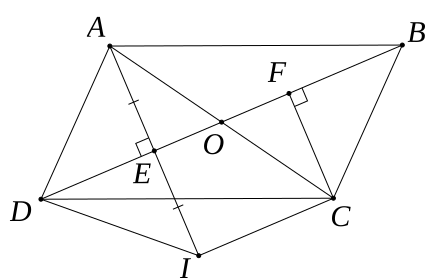
a) Hình bình hành ABCD có O là giao điểm của AC và BD
⇒ O là trung điểm của AC và BD.
⇒ OA = AC và OB = OD
Xét ΔOEA và ΔOFC có:
OA = OC
\(\widehat {AOE} = \widehat {COF}\) (đối đỉnh)
\(\widehat {AEO} = \widehat {CFO} = 90^\circ \)
⇒ ΔOEA = ΔOFC (cạnh huyền – góc nhọn)
⇒ OE = OF
Xét tứ giác AECF có
OE = OF (cmt)
OA = OC (cmt)
⇒ AECF là hình bình hành (hai đường chéo cắt nhau tại trung điểm của mỗi đường)
b) I là điểm đối xứng của A qua BD
⇒ E là trung điểm của AI ⇒ AE = EI
Tam giác AIC có:
O là trung điểm của AC (cmt)
E là trung điểm của AI (cmt)
⇒ OE là đường trung bình tam giác AIC (đpcm)
⇒ OE // IC
c) Xét ΔAID có DE là đường trung trực của AI
⇒ ΔAID cân tại D
⇒ DE cũng là đường phân giác của góc ADI
\( \Rightarrow \widehat {ADE} = \widehat {IDE}\)
mà \(\widehat {ADE} = \widehat {CBF}\) (vì AD//BC)
\( \Rightarrow \widehat {IDE} = \widehat {CBF}\)
Tứ giác CIDB có:
BD // IC (vì OE // IC)
⇒ Tứ giác CIBD là hình than
Mà có \(\widehat {IDE} = \widehat {CBF}\) (cmt)
⇒ CIBD là hình thang cân. (đpcm)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
A = (x – 3)(4x + y) – 4x(x – 3) với x = 1; \(y = - \frac{1}{3}\).