17 câu hỏi trắc nghiệm thuộc Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 7)

Câu 1:

Phân tích đa thức 4x²– 9 thành nhân tử được kết quả là:

A. (4x – 9)(4x + 9);

B. (2x – 3)(2x + 3);

C. (2x – 9)(2x + 9);

D. Đáp án khác.

Xem đáp án

Đáp án đúng là: B

4x²– 9 = (2x)²– 3²= (2x – 3)(2x + 3)

Câu 2:

Tích của đơn thức – x²và đa thức – x²+ 12x – 3 là:

A. – x⁴+ 12x³– 3x²;

B. – x⁴– 12x³– 3x²;

C. x⁴+ 12x³– 3x²;

D. x⁴– 12x³+ 3x².

Xem đáp án

Đáp án đúng là: D

(– x²)(– x²+ 12x – 3) = x⁴– 12x³+ 3x²

Câu 3:

Kết quả phân tích đa thức 2x(x + 5) – (x + 5) thành nhân tử:

A. 2x(x + 5);

B. (x + 5)(2x + 1);

C. (x + 5)(2x – 1);

D. x(x + 5).

Xem đáp án

Đáp án đúng là: C

2x(x + 5) – (x + 5)

= (x + 5)(2x – 1)

Câu 4:

Kết quả thu gọn của biểu thức A = (2x – y)(4x²+ 2xy + y²).

A. 2x³– y³;

B. 2x³+ y³;

C. 8x³– y³;

D. 8x³+ y³.

Xem đáp án

Đáp án đúng là: C

A = (2x – y)(4x²+ 2xy + y²) = (2x)³– y³= 8x³– y³

Câu 5:

Tìm x biết x²+ 25 = 10x.

A. x = 6;

B. x = 5;

C. x = 4;

D. x = 3.

Xem đáp án

Đáp án đúng là: B

x²+ 25 = 10x

x²– 10x + 25 = 0

(x – 5)²= 0

x – 5 = 0

x = 5

Câu 6:

Giá trị của biểu thức x²– 4x + 4 tại x = – 2.

A. 0;

B. – 8;

C. – 16;

D. 16.

Xem đáp án

Đáp án đúng là: D

^x²– 4x + 4 = (x – 2)²

Tại x = – 2 ta có: (– 2 – 2)²= (– 4)²= 16

Câu 7:

Đường trung bình của hình thang có độ dài 6,5 cm, độ dài đáy nhỏ là 5 cm. Độ dài đáy lớn là:

A. 8 cm;

B. 1,5 cm;

C. 11,5 cm;

D. 3,5 cm.

Xem đáp án

Đáp án đúng là: A

Đường TB = (đáy lớn + đáy nhỏ) : 2

⇒ đáy lớn = 2.đường TB – đáy nhỏ

= 2.6,5 – 5

= 8 (cm)

Câu 8:

Cho đoạn thẳng AB có độ dài 5 cm và đường thẳng d, đoạn thẳng A’B’ đối xứng với AB qua d. Khi đó độ dài của A’B’ là:

A. 5 cm;

B. 2,5 cm;

C. 10 cm;

D. 15 cm.

Xem đáp án

Đáp án đúng là: A

Tính chất: Nếu hai đoạn thẳng đối xứng với nhau qua một đường thẳng thì chúng bằng nhau.

⇒ A’B’ = AB = 5cm.

Câu 9:

Tứ giác ABCD là hình bình hành nếu:

A. AB = CD;

B. 2AD = BC;

C. AB // CD và AD = BC;

D. AB = CD và AD = BC.

Xem đáp án

Đáp án đúng là: D

Tứ giác có các cạnh đối bằng nhau là hình bình hành

Tứ giác ABCD có AB = CD và AD = BC thì ABCD là hình bình hành.

Câu 10:

Hình thang cân ABCD (AB//CD) có \(\widehat D = 70^\circ \). Khẳng định nào dưới đây là đúng?

A. \(\widehat A = 110^\circ \);

B. \(\widehat B = 70^\circ \);

C. \(\widehat C = 110^\circ \);

D. \(\widehat A = 70^\circ \).

Xem đáp án

Đáp án đúng là: A

Hình thang cân có hai góc kề 1 đáy bằng nhau

\( \Rightarrow \widehat A = \widehat B\)và \(\widehat D = \widehat C\)

\( \Rightarrow \widehat D = \widehat C = 70^\circ \)

Vì AB // CD nên \[\widehat A + \widehat D = 180^\circ \Rightarrow \widehat A = 180^\circ - \widehat D = 180^\circ - 70^\circ = 80^\circ \]

\( \Rightarrow \widehat A = \widehat B = 110^\circ \)

Câu 11:

Cho tam giác ABC có MN là đường trung bình (MN//AC). Biết MN=4cm. Tính AC = ?

A. 2 cm;

B. 4cm;

C. 8 cm;

D. 16 cm.

Xem đáp án

Đáp án đúng là: C

MN là đường trung bình có MN // AC

\( \Rightarrow MN = \frac{1}{2}AC\)

⇒ AC = 2MN = 2.4 = 8 cm.

Câu 12:

Trong các khẳng định sau đây, khẳng định nào sai?

A. Trung điểm của một đoạn thẳng là tâm đối xứng của đoạn thẳng đó.

B. Giao điểm hai đường chéo của một hình bình hành là tâm đối xứng của hình bình hành đó.

C. Trọng tâm của một tam giác là tâm đối xứng của tam giác đó.

D.Tâm của một đường tròn là tâm đối xứng của đường tròn đó.

Xem đáp án

Đáp án đúng là: C

Tam giác không có tâm đối xứng nên trọng tâm của một tam giác không phải là tâm đối xứng của tam giác đó.

II. TỰ LUẬN (7 điểm)

Câu 13:

Rút gọn biểu thức rồi tính giá trị của biểu thức sau:

A = (x – 3)(4x + y) – 4x(x – 3) với x = 1; \(y = - \frac{1}{3}\).

Xem đáp án

Hướng dẫn giải

A = (x – 3)(4x + y) – 4x(x – 3)

= (x – 3)(4x + y – 4x)

= (x – 3).y

Với x = 1; \(y = - \frac{1}{3}\) ta có: \[A = \left( {1--3} \right).\left( { - \frac{1}{3}} \right) = \frac{2}{3}\].

Câu 14:

Phân tích đa thức thành nhân tử:

a) 15xy + 20xy²;

b) 4x²– y²+ 4x + 1.

Xem đáp án

Hướng dẫn giải

^{a) 15xy + 20xy}²

= 5xy(3 + 4y)

b) 4x²– y²+ 4x + 1

= (4x²+ 4x + 1) – y²

= (2x + 1)²– y²

= (2x + 1 – y)(2x + 1 + y)

Câu 15:

(1 điểm):

Tìm x:

a) 2(x + 3) – x²– 3x = 0

b) x³– 4x = 0

Xem đáp án

Hướng dẫn giải

a) 2(x + 3) – x²– 3x = 0

2(x + 3) – x(x + 3) = 0

(x + 3)(2 – x) = 0

\( \Rightarrow \left[ \begin{array}{l}x + 3 = 0\\2 - x = 0\end{array} \right.\)

\( \Rightarrow \left[ \begin{array}{l}x = - 3\\x = 2\end{array} \right.\)

Vậy x = – 3 và x = 2.

b) x³– 4x = 0

x(x²– 4) = 0

x(x – 2)(x + 2) = 0

\( \Rightarrow \left[ \begin{array}{l}x = 0\\x - 2 = 0\\x + 2 = 0\end{array} \right.\)

\( \Rightarrow \left[ \begin{array}{l}x = 0\\x = 2\\x = - 2\end{array} \right.\)

Vậy x = 0, x = 2 và x = – 2.

Câu 16:

Cho hình bình hành ABCD (AD < AB), O là giao điểm hai đường chéo AC, BD. Gọi E, F lần lượt là hình chiếu của A và C trên BD.

a) Chứng minh tứ giác AECF là hình bình hành.

b) Gọi I là điểm đối xứng của A qua BD. Chúng minh EO là đường trung bình của tam giác AIC.

c) Chứng minh tứ giác CIDB là hình thang cân.

Xem đáp án

Hướng dẫn giải

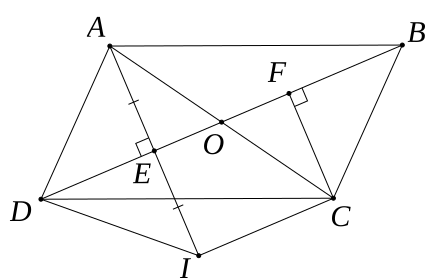
a) Hình bình hành ABCD có O là giao điểm của AC và BD

⇒ O là trung điểm của AC và BD.

⇒ OA = AC và OB = OD

Xét ΔOEA và ΔOFC có:

OA = OC

\(\widehat {AOE} = \widehat {COF}\) (đối đỉnh)

\(\widehat {AEO} = \widehat {CFO} = 90^\circ \)

⇒ ΔOEA = ΔOFC (cạnh huyền – góc nhọn)

⇒ OE = OF

Xét tứ giác AECF có

OE = OF (cmt)

OA = OC (cmt)

⇒ AECF là hình bình hành (hai đường chéo cắt nhau tại trung điểm của mỗi đường)

b) I là điểm đối xứng của A qua BD

⇒ E là trung điểm của AI ⇒ AE = EI

Tam giác AIC có:

O là trung điểm của AC (cmt)

E là trung điểm của AI (cmt)

⇒ OE là đường trung bình tam giác AIC (đpcm)

⇒ OE // IC

c) Xét ΔAID có DE là đường trung trực của AI

⇒ ΔAID cân tại D

⇒ DE cũng là đường phân giác của góc ADI

\( \Rightarrow \widehat {ADE} = \widehat {IDE}\)

mà \(\widehat {ADE} = \widehat {CBF}\) (vì AD//BC)

\( \Rightarrow \widehat {IDE} = \widehat {CBF}\)

Tứ giác CIDB có:

BD // IC (vì OE // IC)

⇒ Tứ giác CIBD là hình than

Mà có \(\widehat {IDE} = \widehat {CBF}\) (cmt)

⇒ CIBD là hình thang cân. (đpcm)

Câu 17:

Tìm giá trị lớn nhất của biểu thức: A = 12 – x²– 6x.

Xem đáp án

Hướng dẫn giải

A = 12 – x²– 6x

= –(x²+ 6x – 12)

= –(x²+ 6x + 9 – 21)

= –(x + 3)²+ 21

Có (x + 3)²≥ 0 \(\forall x \in \mathbb{R}\)

⇒ –(x + 3)²≤ 0 \(\forall x \in \mathbb{R}\)

⇒ –(x + 3)²+ 21 ≤ 21 \(\forall x \in \mathbb{R}\)

⇒ A ≤ 21

Dấu “=” xảy ra khi (x + 3)²= 0

⇔ x + 3 = 0

⇔ x = – 3

Vậy giá trị lớn nhất của A = 21 khi x = – 3.

CHỌN BỘ SÁCH BẠN MUỐN XEM

Đề thi Giữa kì 1 Toán 8 có đáp án

Đề thi Giữa kì 1 Toán 8 có đáp án (Đề 7)

Danh sách câu hỏi

Bài thi liên quan

Có thể bạn quan tâm

Các bài thi hot trong chương