Căn hộ nhà bác Cường diện tích 105. Ngoại trừ bếp và nhà vệ sinh diện tích 30, toàn bộ diện tích sàn còn lại được lát gỗ như sau: 18 được lát bằng gỗ loại 1 giá 350 nghìn đồng/, phần còn lại dùng bằng gỗ loại 2 có giá 170 nghìn đồng/. Công lát là 30 nghìn đồng/
Viết biểu thức tính tổng chi phí bác Cường cần trả để lát sàn căn hộ như trên. Tính giá trị của biểu thức đó.
A. 15 990 000 đồng.
B. 2 250 000 đồng.
C. 18 240 000 đồng.
D. 9 690 000 đồng.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án C
Diện tích sàn được lát gỗ là: 105 – 30 = 75 ()
Diện tích sàn lát gỗ loại 2 là: 75 – 18 = 57 ()
Chi phí mua gỗ loại 1 là: 350 000. 18 = 6 300 000 (đồng)
Chi phí mua gỗ loại 2 là: 170 000. 57 = 9 690 000 (đồng)
Chi phí trả công lát gạch là: 30 000. 75 = 2 250 000 (đồng)
Biểu thức tính tổng chi phí bác Cường cần trả để lát sàn là:
6 300 000 + 9 690 000 + 2 250 000
= 15 990 000 + 2 250 000
= 18 240 000 (đồng)
Vậy tổng chi phí bác Cường cần trả để lát sàn căn hộ trên là 18 240 000 đồng.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Cho phép tính 12 + 8.3. Bạn Nam thực hiện như sau:
12 + 8.3
= (12 + 8).3 (Bước 1)
= 20.3 (Bước 2)
= 60. (Bước 3)
Bạn Nam sai từ bước nào?
Thứ tự thực hiện phép tính nào sau đây là đúng đối với biểu thức không có dấu ngoặc?
Một người đi xe đạp trong 5 giờ. Trong 3 giờ đầu, người đó đi với vận tốc 14km/h; 2 giờ sau, người đó đi với vận tốc 9km/h.
a) Tính quãng đường người đó đi được trong 3 giờ đầu; trong 2 giờ sau.
b) Tính quãng đường người đó đi được trong 5 giờ.
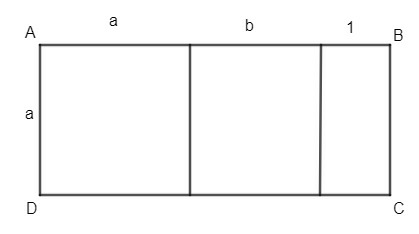
Tính diện tích hình chữ nhật ABCD (hình bên) với a = 10cm, b = 7 cm.
Một người đi xe đạp trong 5 giờ. Trong 3 giờ đầu, người đó đi với vận tốc 14km/h; 2 giờ sau, người đó đi với vận tốc 9km/h. Tính quãng đường người đó đi được trong 5 giờ.
Thứ tự thực hiện phép tính nào sau đây là đúng đối với biểu thức có dấu ngoặc?
+ Đối với các biểu thức không có dấu ngoặc:
- Nếu chỉ có phép cộng và phép trừ (hoặc chỉ có phép nhân và phép chia) thì thực hiện các phép tính từ trái qua phải.
- Nếu có các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa thì ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân và chia, cuối cùng đến cộng và trừ.
Ví dụ 1. Tính giá trị biểu thức sau:
a) 23 + 47 – 52;
b) 24.5:3;
c) 22.3 + 3.7 – 18:9.
Lời giải
a) 23 + 47 – 52
= 70 – 52
= 18.
b) 24.5:3
= 120 : 3
= 40.
c) 22.3 + 3.7 – 18:9
= 4.3 + 21 – 2
=12 + 21 – 2
= 33 – 2
= 31.
+ Đối với các biểu thức có dấu ngoặc:
- Nếu chỉ có một dấu ngoặc thì ta thực hiện phép tính trong dấu ngoặc trước.
- Nếu có các dấu ngoặc tròn (), dấu ngoặc vuông [], dấu ngoặc nhọn {} thì ta thực hiện các phép tính trong dấu ngoặc tròn trước, rồi thực hiện các phép tính trong dấu ngoặc vuông, cuối cùng thực hiện các phép tính trong dấu ngoặc nhọn.
Ví dụ 2. Thực hiện phép tính
a) (30 + 80).2 + 20:4;
b) :2
Lời giải
a) (30 + 80).2 + 20:4
= 110.2 + 5
= 220 + 5
= 225.
b) :2
= :2
= :2
= :2
= 20:2
=10.
B. Bài tập
Bài 1. Tính giá trị của biểu thức:
a) 36 – 18:6;
b) 2.32 – 24:(6.2);
c) 120 + [55 – (11 – 3.2)2] + 23.
Lời giải
a) 36 – 18:6 = 36 – 3 = 33
b) 2.32 – 24:(6.2)
= 2.9 – 24:12
= 18 – 2
= 16
c) 120 + [55 – (11 – 3.2)2] + 23
= 120 + [55 – (11 – 6)2] + 23
= 120 + [55 – (5)2] + 23
= 120 + [55 – 25] + 8
= 120 + 30 + 8
= 158.
Bài 2. Tính giá trị của biểu thức:
a) 1 + 2(a + b) – 43 khi a = 25; b = 9;
b) [2.x – (23.4 - 16):y].1230 khi x = 8; y = 1.
Lời giải
a) Thay a = 25; b = 9 vào biểu thức ta được:
1 + 2(25 + 9) – 43
= 1 + 2.34 – 64
= 1 + 68 – 64
= 69 – 64
= 5
b) Thay x = 8, y = 1 vào biểu thức, ta được:
[2.8 – (23.4 - 16):1].1230
= [16 – (8.4 - 16):1].1230
= [16 – (32 - 16):1].1230
= [16 – 16:1].1230
= [16 – 16].1230
= 0:1230
= 0