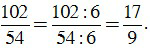Nếu 9 là số lớn nhất sao cho $\mathrm{a}⋮9$ và $\mathrm{b}⋮9$ thì 9 là ………… của a và b. Chọn câu trả lời đúng nhất.

1. Ước chung và ước chung lớn nhất

Ước chung của hai hay nhiều số là ước của tất cả các số đó.

Ước chung lớn nhất của hai hay nhiều số là số lớn nhất trong tập hợp các ước chung của các số đó.

Ta kí hiệu:

ƯC(a, b) là tập hợp các ước chung của a và b.

ƯCLN(a, b) là ước chung lớn nhất của a và b.

Ví dụ 1. 

a) Tìm ước chung của 24 và 60.

b) Tìm ƯCLN (24; 60).

Lời giải

Ư(24) = {1; 2; 3; 4; 6; 8; 12; 24}

Ư (30) = {1; 2; 3; 5; 6; 10; 15; 30}

a) ƯC(24; 30) = {1; 2; 3; 6}

b) ƯCLN(24; 30) = 6.

Nhận xét: 

- Trong các số đã cho, nếu số nhỏ nhất là ước của các số còn lại thì ƯCLN của các số đã cho chính là số nhỏ nhất ấy.

Nếu a 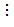  b thì ƯCLN(a, b) = b.

- Số 1 chỉ có 1 ước là 1. Do đó với mọi số tự nhiên a và b, ta có: 

ƯCLN(a, 1) = 1; ƯCLN(a, b, 1) = 1.

Ví dụ 2. 

a) Tìm ƯCLN(180, 18)

Vì 180 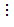 18 nên ƯCLN(180, 18) = 18.

b) Tìm ƯCLN(13, 1)

Ta có: ƯCLN(13, 1) = 1.

2. Cách tìm ước chung lớn nhất

Các bước tìm ƯCLN của hai hay nhiều số lớn hơn 1:

Bước 1: Phân tích các số ra thừa số nguyên tố.

Bước 2: Chọn ra các thừa số nguyên tố chung.

Bước 3. Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ nhỏ nhất. Tích đó là ƯCLN phải tìm.

Ví dụ 3. Cách tìm ƯCLN(140, 168)

Ta có: 140 = 2².5.7;   168 = 2³.3.7.

Các thừa số chung: 2, 7.

Vậy ƯCLN(140, 168) = 2².7 = 4.7 = 28.

3. Rút gọn về phân số tối giản

Vận dụng ƯCLN để rút gọn về phân số tối giản

Ta rút gọn phân số bằng cách chia cả tử và mẫu của phân số đó cho một ước chung khác 1 (nếu có).

Phân số 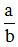  được gọi là phân số tối giản nếu a và b không có ước chung nào khác 1, nghĩa là ƯCLN(a, b) = 1.

Ví dụ 4. Rút gọn các phân số sau về phân số tối giản

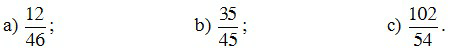
Lời giải

a) ƯCLN(12, 46) = 2.

Để rút gọn phân số ta chia cả tử và mẫu cho ƯCLN của 12 và 46, ta được:

;

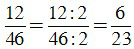b) ƯCLN(35,45) = 5.

Để rút gọn phân số ta chia cả tử và mẫu cho ƯCLN của 35 và 45, ta được:

 ;

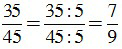c) ƯCLN(102, 54) = 6.

Để rút gọn phân số ta chia cả tử và mẫu cho ƯCLN của 102 và 54, ta được: