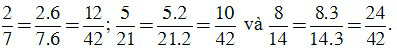Thực hiện các phép tính sau:

a) $\frac{7}{11}+\frac{5}{7}$

b) $\frac{7}{20}-\frac{2}{15}$

1. Bội chung và bội chung nhỏ nhất

Bội chung của hai hay nhiều số là bội của tất cả các số đã cho.

Bội chung nhỏ nhất của hai hay nhiều số là số nhỏ nhất khác 0 trong tập hợp các bội chung của các số đó.

Kí hiệu:

BC(a, b) là tập hợp các bội chung của a và b.

BCNN(a, b) là bội chung nhỏ nhất của a và b.

Ví dụ 1. Tìm bội chung và bội chung nhỏ nhất của 30 và 45

Lời giải 

Ta có B(30) = {0; 30; 60; 90; 120; 150; 180; 210; 240; 270; …}

B(45) = {0; 45; 90; 135; 180; 225; 270; …}

BC(30, 45) = {0; 90; 180; 270; …}.

BCNN(30, 45) = 90.

Nhận xét: Trong các số đã cho, nếu số lớn nhất là bội của các số còn lại thì BCNN của các số đã cho chính là số lớn nhất đó. 

Nếu a 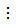b thì BCNN(a, b) = a.

Mọi số tự nhiên đều là bội của 1. Do đó với mọi số tự nhiên a và b (khác 0), ta có: 

BCNN(a, 1) = a; BCNN(a, b, 1) = BCNN(a, b).

Ví dụ 2. Tìm bội chung nhỏ nhất của các số sau:

a) 12 và 36;

b) 124 và 1.

Lời giải

a) Vì 36 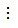12 nên BCNN(12, 36) = 36;

b) Vì 124 là bội của 1 nên BCNN(1; 124) = 124.

2. Cách tìm bội chung nhỏ nhất

Các bước tìm BCNN của hai hay nhiều số lớn hơn 1:

Bước 1. Phân tích mỗi số ra thừa số nguyên tố;

Bước 2. Chọn ra các thừa số nguyên tố chung và riêng;

Bước 3. Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất. Tích đó là BCNN cần tìm.

Ví dụ 3. Tìm bội chung nhỏ nhất của 21 và 14.

Lời giải

Ta có 21 = 3.7; 14 = 2.7.

Khi đó BCNN(21, 14) = 2.3.7 = 42.

Tìm bội chung từ bội chung nhỏ nhất

Để tìm bội chung của các số đã cho ta có thể làm như sau:

Bước 1. Tìm BCNN của các số đã cho.

Bước 2. Tìm các bội của BCNN đó.

Ví dụ 4. Tìm BC(12, 24, 30) 

Lời giải

Ta có: 12 = 2².3; 24 = 2³.3; 30 = 2.3.5.

BCNN(12, 24, 30) = 2³.3.5 = 120.

BC(12, 24, 30) = B(120) = {0; 120; 240; 360; 480; …}.

3. Quy đồng mẫu các phân số

Vận dụng BCNN để tìm mẫu chung của hai phân số:

Để quy đồng mẫu số hai phân số 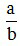  và 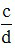 , ta phải tìm mẫu chung của hai phân số đó. Thông thường ta nên chọn mẫu chung là BCNN của hai mẫu.

Ví dụ 5. Quy đồng mẫu số các phân số sau:

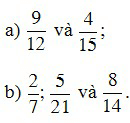
Lời giải

a) Ta có 12 = 2².3; 15 = 3.5.

BCNN(12, 15) = 2².3.5 = 60.

Ta có: 60:12 = 5; 60:15 = 4. Khi đó:

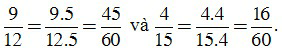
b) Ta có: 7 = 7, 21 = 3. 7, 14 = 2.7.

BCNN(7, 21, 14) = 2.3.7 = 42.

Ta có: 42:7 = 6, 42:21 = 2, 42:14 = 3. Khi đó: