Cho tập hợp H = {0; 1; 2; 4; 5; 7; 9}. Tập hợp K là tập hợp gồm các số đối của phần tử của tập hợp H. Tìm tập hợp K.
A. K = {0; -1; -2; -4; -5; -7; -9}.
B. K = {-0; -1; -2; -4; -5; -7; -9}.
C. K = {-1; -2; -4; -5; -7; -9}.
D. K = { -1; -2; -4; -5; -7; -9; 0; 1; 2; 4; 5; 7; 9}.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án A
Số đối của 0 là 0;
Số đối của 1 là -1;
Số đối của 2 là – 2;
Số đối của 4 là -4;
Số đối của 5 là -5;
Số đối của 7 là -7;
Số đối của 9 là -9.
Vậy tập hợp K = {0; -1; -2; -4; -5; -7; -9}.
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Tìm các số nguyên x thỏa mãn – 12 < x < 13. Có bao nhiêu số nguyên như vậy?
Cho bảng nhiệt độ của các thành phố lớn của nước ta:
Thành phố | Hà Nội | Huế | Phan Thiết | Hồ Chí Minh |
Nhiệt độ |
Hỏi nhiệt độ của tỉnh thành nào thấp nhất?
Liệt kê các phần tử của mỗi tập hợp sau:
a) {x ∈ Z|-2 ≤ X < 4}
b) {x ∈ Z|-2 < X ≤ 4}
Trên trục số, mỗi điểm sau nằm cách gốc O bao nhiêu đơn vị?
a) Điểm 2; b) Điểm – 4.
Sắp xếp các số sau theo thứ tự tăng dần:
- 3; 4; -9; 0; -12; 2; 15; 1.
1. Làm quen với số nguyên âm
- Các số tự nhiên (khác 0) 1; 2; 3; 4; … còn được gọi là các số nguyên dương.
- Các số - 1; -2; -3; … gọi là các số nguyên âm.
- Tập hợp gồm các số nguyên âm, số 0 và số nguyên dương gọi là tập hợp số nguyên.
Z = {...; -3; -3; -3; 0; 1; 2; 3;...}.
Chú ý:
Số 0 không là số nguyên âm, cũng không phải là số nguyên dương.
Đôi khi ta còn viết thêm dấu “+” ngay trước một số nguyên dương. Chẳng hạn số 6 còn được viết là +6 (đọc là “dương sáu”).
Ví dụ 1. Các số nguyên nào biểu diễn các đại lượng sau:
a) Đỉnh núi Phan – xi – păng cao 3 147, 3m;
b) Độ sâu của đáy sông Sài Gòn là 20m;
c) Bác An đang nợ 2 triệu đồng.
Lời giải
a) Độ cao củ đỉnh núi Phan – xi – păng được biểu diễn là: 3 147, 3m.
b) Độ sâu của đáy sông Sài Gòn được biểu diễn là: -20 m.
c) Số tiền nợ của bác An được biểu diễn là: - 2 (triệu đồng).
2. Thứ tự trong tập số nguyên
Trục số:
Ta biểu diễn các số 0; 1; 2; 3; 4; 5 … và các số nguyên âm -1; -2; -3; 4; 5… như sau:
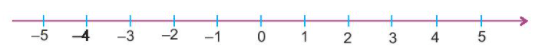
+ Chiều từ trái sang phải là chiều dương, chiều ngược lại là chiều âm.
+ Điểm biểu diễn số nguyên a được gọi là điểm a.
+ Cho hai số nguyên a và b. Trên trục số, nếu điểm a nằm trước điểm b thì số a nhỏ hơn số b, kí hiệu a < b.
Ví dụ 2. Các điểm A, B, C, D và E trong hình biểu diễn những số nào?

Lời giải
Điểm A cách điểm 0 năm đơn vị về bên phải nên A biểu diễn cho số 5;
Điểm C cách điểm 0 bảy đơn vị về bên phải nên C biểu diễn cho số 7;
Điểm B cách điểm 0 bốn đơn vị về bên trái nên B biểu diễn cho số -4;
Điểm E biểu diễn cho điểm – 1;
Điểm D biểu diễn cho điểm 0;
So sánh hai nguyên:
Mọi số nguyên âm đều nhỏ hơn 0, do đó nhỏ hơn mọi số nguyên dương.
Nếu a, b là hai số nguyên dương và a > b thì – a < - b.
Ví dụ 2. Sắp xếp các số sau theo thứ tự tăng dần:
- 3; 4; -9; 0; -12; 2; 15; 1.
Lời giải
Các số đã cho được sắp xếp theo thứ tự tăng dần là:
-12; -9; -3; 0; 1; 2; 4; 15.
B. Bài tập
Bài 1. Liệt kê các phần tử của mỗi tập hợp sau:
a) B = {x ∈ Z | -3 ≤ x ≤ 4} ;
b) B = {x ∈ Z | -2 ≤ x ≤ 0}.
Lời giải
a) A = {-3; -2; -1; 0; 1; 2; 3}.
b) B = {-2; -1; 0}.
Bài 2. So sánh hai số:
a) -49 và -38; b) -1379 và – 2379.
Lời giải
a) Vì 49 > 38 nên -49 < -38.
b) Vì 2379 > 1379 nên -2379 < -1379.
Bài 3. Hãy sử dụng số nguyên âm để diễn tả lại ý nghĩa của các câu sau:
a) Mùa đông ở Siberia (Nga) dài và khắc nghiệt, với nhiệt độ trung bình tháng 1 là 25oC dưới 0oC .
b) Cá voi xanh có thể lặn sâu 2500m có với mực nước biển.
Lời giải
a) Nhiệt độ trung bình tháng 1 của Siberia (Nga) được biểu diễn là: -25oC .
b) Độ sâu mà Cá voi xanh có thể lặn được biểu diễn là: – 2500 m.