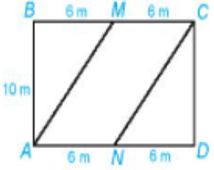
Trên một mảnh đất hình chữ nhật có chiều dài 12m, chiều rộng 10m, người ta phân chia khu vực để trồng hoa, trồng cỏ như hình bên. Hoa sẽ được trồng ở trong khu vực hình bình hành AMCN, cỏ sẽ trồng ở phần đất còn lại. Tiền công để trả cho mỗi mét vuông trồng hoa là 50 000 đồng, trồng cỏ là 40 000 đồng. Tính số tiền công cần chi trả để trồng hoa và cỏ.
 Giải bởi Vietjack
Giải bởi Vietjack
Dễ thấy trong hình bình hành AMCN chiều cao tương ứng của cạnh AN là MN và MN = AB = 10m
Do đó diện tích hình bình hành AMCN là:
6. 10 = 60 ()
Diện tích hình chữ nhật ABCD là:
10. 12 = 120 ()
Phần diện tích còn lại trồng cỏ là:
120 - 60 = 60 ()
Số tiền công cần để chi trả trồng hoa là:
50 000. 60 = 3 000 000 (đồng)
Số tiền công cần để chi trả trồng cỏ là:
40 000. 60 = 2 400 000 (đồng)
Số tiền công cần để chi trả trồng hoa và cỏ là:
3 000 000 + 2 400 000 = 5 400 000 (đồng)
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Một ngôi nhà có bãi có bảo quanh như hình bên.
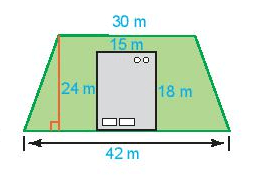
a) Hãy tính diện tích của bãi cỏ.
b) Nếu một túi hạt giống cỏ gieo vừa đủ trên 54m2 đất, thì cần bao nhiêu túi hạt giống để gieo vừa hết bãi cỏ?
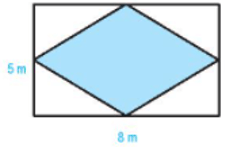
Trong mảnh vườn hình chữ nhật có chiều dài 8 m, chiều rộng 5 m, người ta trồng hoa hồng trong một mảnh đất hình thoi như hình bên. Nếu mỗi mét vuông trồng 4 cây hoa thì cần bao nhiêu cây hoa để trồng trên mảnh đất hình thoi đó?
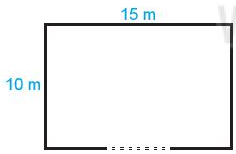
Một khu vườn hình chữ nhật có chiều dài 15m, chiều rộng 10 m như hình dưới, cổng vào có độ rộng bằng chiều dài, phần còn lại là hàng rào. Hỏi hàng rào của khu vườn dài bao nhiêu mét?
Bác Khôi muốn lát nền cho một căn phòng hình chữ nhật có chiều dài 6m, chiều rộng 3m. Loại gạch lát nền được sử dụng là hình vuông có cạnh 30cm. Hỏi bác Khôi phải sử dụng bao nhiêu viên gạch (coi mạch vữa không đáng kể).
Diện tích của một hình thoi là 100 và một đường chéo dài 20 dm. Độ dài đường chéo còn lại là:
Cho hình thang cân có tổng hai đáy bằng 18 dm và chu vi hình thang cân 340 cm. Độ dài cạnh bên của hình thang cân là:
Một gia đình dự định mua gạch men loại hình vuông cạnh 30 cm để lát nền của căn phòng hình chữ nhật có chiều rộng 3 m, chiều dài 9 m. Tính số viên gạch cần mua để lát căn phòng đó.
Diện tích hình bình hành có chiều dài một cạnh 20 cm và chiều cao tương ứng 5 cm là:
Một mảnh ruộng hình thang có kích thước như hình dưới. Biết năng suất lúa là 0,8 kg/.
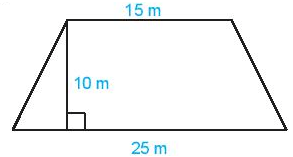
a) Tính diện tích mảnh ruộng.
b) Hỏi mảnh ruộng cho sản lượng là bao nhiêu kilogam thóc?
Hình chữ nhật có chu vi bằng 28 cm. Tính diện tích của hình chữ nhật đó biết chiều dài hơn chiều rộng 6cm.
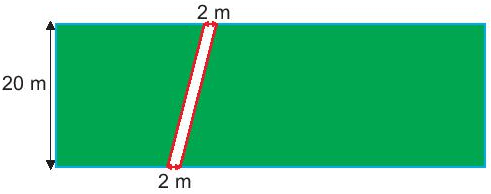
Trong một khu vườn hình chữ nhật, người ta làm một lối đi lát sỏi với các kích thước như hình vẽ sau. Chi phí cho mỗi mét vuông làm lối đi hết 120 nghìn đồng. Hỏi chi phí để làm lối đi là bao nhiêu?
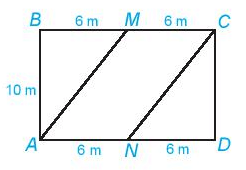
Trên một mảnh đất hình chữ nhật có chiều dài 12m, chiều rộng 10m.
a) Người nông dân định làm một tường rào bao quanh khu vườn. Hỏi tường rào đó dài bao nhiêu m?
b) Trên khu vườn nó người nông dân phân chia khu vực để trồng hoa, trồng cỏ như hình bên. Hoa sẽ được trồng ở khu vực hình bình hành AMCN, cỏ sẽ được trồng ở phần đất còn lại. Tính diện tích trồng hoa và trồng cỏ.
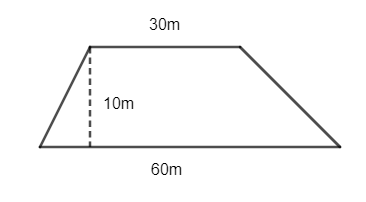
Một thửa ruộng có dạng như hình bên. Nếu trên mỗi mét vuông thu hoạch được 0,8kg thóc thì thửa ruộng đó thu hoạch được bao nhiêu ki – lô – gam thóc?
Hình thang cân có độ dài hai cạnh đáy là 5 m và 3,2 m; chiều cao là 4 m. Diện tích của hình thang cân này là:
1. Chu vi, diện tích của hình vuông, hình chữ nhật, hình thang
Công thức:
Hình vuông cạnh a:
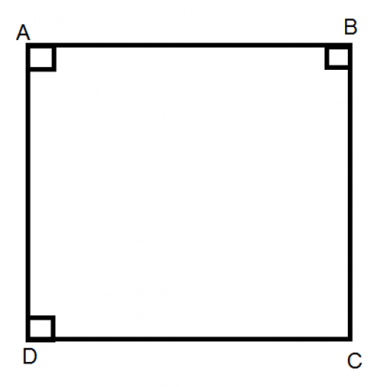
Chu vi: C = 4a.
Diện tích: S = a2.
Hình chữ nhật có chiều dài là a, chiều rộng là b:
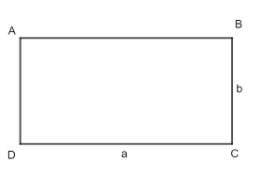
Chu vi: C = 2(a + b).
Diện tích: S = a.b.
Hình thang có độ dài hai cạnh đáy là a, b chiều cao h:
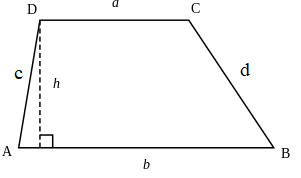
Chu vi: C = a + b + c + d.
Diện tích: S = (a + b).h:2.
Ví dụ 1. Bác Khôi muốn lát nền cho một căn phòng hình chữ nhật có chiều dài 6m, chiều rộng 3m. Loại gạch lát nền được sử dụng là hình vuông có cạnh 30cm. Hỏi bác Khôi phải sử dụng bao nhiêu viên gạch (coi mạch vữa không đáng kể).
Lời giải
Diện tích căn phòng hình chữ nhật là: 6.3 = 18 (m2).
Diện tích một viên gạch lát nền là: 30.30 = 900(cm2).
Đổi 18 m2 = 180 000 (cm2).
Số viên gạch cần để lát đủ căn phòng là: 180 000:900 = 200 (viên).
Ví dụ 2. Một thửa ruộng có dạng như hình bên. Nếu trên mỗi mét vuông thu hoạch được 0,8kg thóc thì thửa ruộng đó thu hoạch được bao nhiêu ki – lô – gam thóc?

Lời giải
Diện tích thửa ruộng hình thang là: (60 + 30).10:2 = 450 (m2).
Trên thửa ruộng đó thu hoạch được số ki – lô – gam thóc là: 450.0,8 = 360 (kg).
Vậy trên thửa ruộng đó thu hoạch được 360 ki – lô – gam thóc.
2. Chu vi, diện tích hình bình hành, hình thoi.
Hình bình hành:
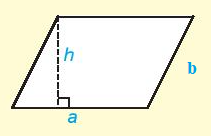
Chu vi: C = 2(a + b).
Diện tích: S = a.h.
Hình thoi:
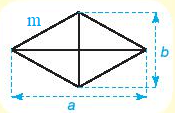
Chu vi: C = 4.m.
Diện tích: S = 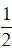 ab .
ab .
Ví dụ 3. Trên một mảnh đất hình chữ nhật có chiều dài 12m, chiều rộng 10m.
a) Người nông dân định làm một tường rào bao quanh khu vườn. Hỏi tường rào đó dài bao nhiêu m?
b) Trên khu vườn nó người nông dân phân chia khu vực để trồng hoa, trồng cỏ như hình bên. Hoa sẽ được trồng ở khu vực hình bình hành AMCN, cỏ sẽ được trồng ở phần đất còn lại. Tính diện tích trồng hoa và trồng cỏ.

Lời giải
a) Chu vi của khu vườn hình chữ nhật là: 2.(12 + 10) = 2.22 = 44 (m).
Vậy độ dài của tường rào là: 44m.
b) Diện tích trồng hoa là: 6.10 = 60 (m2).
Diện tích khu vườn hình chữ nhật: 12.10 = 120 (m2).
Diện tích trồng cỏ là: 120 – 60 = 60 (m2).
Ví dụ 4. Hình thoi MNPQ có độ dài hai đường chéo 5m và 4m. Diện tích hình thoi MNPQ bằng bao nhiêu?
Lời giải
Diện tích hình thoi MNPQ là: 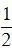 .5.4 = 10(m2) .
.5.4 = 10(m2) .
Vậy diện tích hình thoi MNPQ là 10 m2.