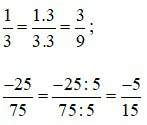Chia cả tử và mẫu của phân số cho 7 ta được phân số nào? Phân số vừa tìm được có bằng phân số không?
Giải bởi Vietjack
Chia cả tử và mẫu của phân số cho 7 ta được:
Ta có: (-28). 3 = - (28. 3) = -84
21. (-4) = - (21. 4) = -84
Vì (-28). 3 = 21. (-4) = -84 nên
Vậy khi chia cả tử và mẫu của phân số cho 7 ta được phân số bằng phân số
Gói VIP thi online tại VietJack (chỉ 400k/1 năm học), luyện tập gần 1 triệu câu hỏi có đáp án chi tiết
Viết kết quả của các phép chia sau dưới dạng phân số.
a) 4: 9;
b) (-2): 7;
c) 8: (-3)
Viết các số đo thời gian sau đây theo đơn vị giờ, dưới dạng phân số tối giản.
15 phút; 90 phút.
Cách viết nào sau đây cho ta một phân số? Cho biết tử và mẫu của phân số đó
Trong các phân số , phân số nào là phân số tối giản?
Nếu chưa là phân số tối giản, hãy rút gọn chúng.
Một vòi nước chảy vào một bể không có nước, sau 40 phút thì đầy bể. Hỏi sau 10 phút, lượng nước đã chảy chiếm bao nhiêu phần bể?
Chia hai hình chữ nhật cùng kích thước thành các phần bằng nhau và tô màu như hình 6.1.
Viết phân số biểu thị phần tô màu trong mỗi hình bên.
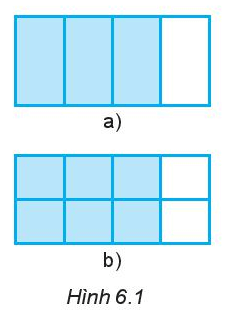
Viết phân số biểu thị phần tô màu trong mỗi hình bên.
a) Cho biết các phân số sau có bằng nhau không?
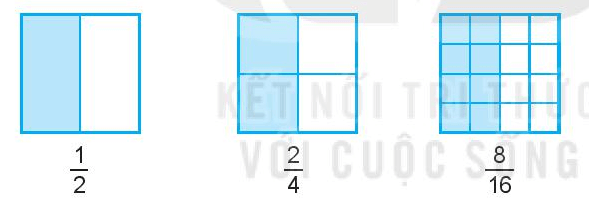
b) Thay các dấu “?” trong hình bên bằng số thích hợp rồi rút ra nhận xét
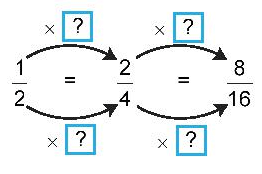
Viết mỗi phân số sau đây thành phân số bằng nó và có mẫu dương.
;
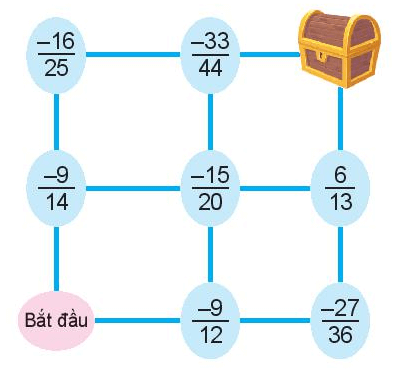
Việt đang chơi trò chơi dò đường. Biết rằng Việt chỉ được phép di chuyển giữa các ô theo đường kẻ và chứa phân số bằng phân số . Em hãy giúp Việt tìm đường đi đên kho báu nhé.
Với mỗi cặp phân số bằng nhau trên, nhân tử số của phân số này với mẫu số của phân số kia rồi so sánh kết quả.
Tìm những cặp phân số bằng nhau trong các phân số sau và sử dụng tính chất cơ bản của phân số để giải thích kết luận.
1. Mở rộng khái niệm về phân số
– Định nghĩa về phân số: Với a, b ∈ ℤ, b ≠ 0 , ta gọi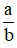 
là một phân số, trong đó a là tử số (tử), b là mẫu số (mẫu) của phân số.
Ví dụ 1:
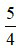là một phân số với tử số là 5 và mẫu số là 4 đọc là năm phần tư.
là một phân số với tử số là –10 và mẫu số là 4 đọc là âm mười phần tư.
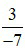là một phân số với tử số là 3 và mẫu số là –7 đọc là ba phần âm bảy.
Chú ý: Mọi số nguyên đều có thể viết dưới dạng phân số.
Ví dụ 2:
Số 3 có thể viết dưới dạng phân số là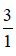 
.
Số –8 có thể viết dưới dạng phân số là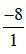 
.
2. Hai phân số bằng nhau
Hai phân số 
và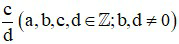 
được gọi là bằng nhau nếu a.d = b.c. Khi đó ta viết là 
.
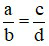Ví dụ 3: Hai phân số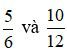 
bằng nhau vì 5.12 = 60 và 6.10 = 60.
3. Tính chất cơ bản của phân số
– Nếu nhân cả tử và mẫu của một phân số với cùng một số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.
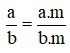với a, b, m ∈ ℤ; b≠0; m≠0.
– Nếu chia cả tử và mẫu của một phân số cho cùng một ước chung của chúng thì ta được một phân số bằng phân số đã cho.
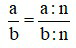với n là ước chung của a và b; a, b, m ∈ ℤ; b≠0 .
Ví dụ 4:
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số chẵn
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 2
Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
